Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T04:52:56.928Z Has data issue: false hasContentIssue false
  • English
  • Français

ZFC PROVES THAT THE CLASS OF ORDINALS IS NOT WEAKLY COMPACT FOR DEFINABLE CLASSES

Published online by Cambridge University Press:  01 May 2018

ALI ENAYAT  and
JOEL DAVID HAMKINS
ALI ENAYAT
Affiliation:
DEPARTMENT OF PHILOSOPHY, LINGUISTICS, & THEORY OF SCIENCE UNIVERSITY OF GOTHENBURG BOX 200, 405 30, GOTHENBURG, SWEDEN E-mail: [email protected] URL: http://flov.gu.se/om/personal?userid=xenaal
JOEL DAVID HAMKINS
Affiliation:
THE GRADUATE CENTER THE CITY UNIVERSITY OF NEW YORK 365 FIFTH AVE NEW YORK, NY 10016, USA and COLLEGE OF STATEN ISLAND THE CITY UNIVERSITY OF NEW YORK 2800 VICTORY BOULEVARD STATEN ISLAND, NY 10314, USA E-mail: [email protected] URL: http://jdh.hamkins.org
Get access Rights & Permissions [Opens in a new window]

Abstract

In ZFC, the class Ord of ordinals is easily seen to satisfy the definable version of strong inaccessibility. Here we explore deeper ZFC-verifiable combinatorial properties of Ord, as indicated in Theorems A & B below. Note that Theorem A shows the unexpected result that Ord is never definably weakly compact in any model of ZFC.

Theorem A. Let 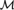${\cal M}$ be any model of ZFC.

  1. (1) The definable tree property fails in 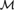${\cal M}$: There is an 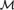${\cal M}$-definable Ord-tree with no 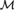${\cal M}$-definable cofinal branch.

  2. (2) The definable partition property fails in 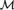${\cal M}$: There is an 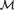${\cal M}$-definable 2-coloring 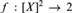$f:{[X]^2} \to 2$ for some 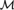${\cal M}$-definable proper class X such that no 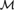${\cal M}$-definable proper classs is monochromatic for f.

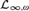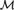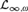  3. (3) The definable compactness property for ${{\cal L}_{\infty ,\omega }}$ fails in ${\cal M}$: There is a definable theory ${\rm{\Gamma }}$ in the logic ${{\cal L}_{\infty ,\omega }}$ (in the sense of 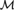${\cal M}$) of size Ord such that every set-sized subtheory of ${\rm{\Gamma }}$ is satisfiable in 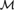${\cal M}$, but there is no 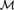${\cal M}$-definable model of ${\rm{\Gamma }}$.

Theorem B. The definable ⋄Ord principle holds in a model 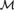${\cal M}$ of ZFC iff 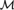${\cal M}$ carries an 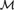${\cal M}$-definable global well-ordering.

Theorems A and B above can be recast as theorem schemes in ZFC, or as asserting that a single statement in the language of class theory holds in all ‘spartan’ models of GB (Gödel-Bernays class theory); where a spartan model of GB is any structure of the form 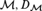$\left( {{\cal M},{D_{\cal M}}} \right)$, where 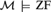${\cal M} \models {\rm{ZF}}$ and 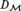${D_{\cal M}}$ is the family of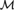${\cal M}$-definable classes. Theorem C gauges the complexity of the collection GBspa of (Gödel-numbers of) sentences that hold in all spartan models of GB.

Theorem C. GBspa is 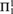${\rm{\Pi }}_1^1$-complete.

Keywords

03E5503C62weakly compact cardinalZermelo-Fraenkel set theoryGödel-Bernays class theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 1 , March 2018 , pp. 146 - 164
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barwise, J., Admissible Sets and Structures, Springer-Verlag, Berlin, 1975.Google Scholar
Devlin, K. D., Constructibility, Springer-Verlag, Berlin, 1984.Google Scholar
Easton, W., Powers of Regular Cardinals, Doctoral dissertation, Princeton University, 1964.Google Scholar
Enayat, A., On certain elementary extensions of models of set theory. Transactions of the American Mathematical Society, vol. 283 (1984), pp. 705–715.Google Scholar
Enayat, A., Power-like models of set theory, this Journal, vol. 66, (2001), pp. 1766–1782.Google Scholar
Enayat, A., Automorphisms, Mahlo cardinals, and NFU, Nonstandard Models of Arithmetic and Set Theory (Enayat, A. and Kossak, R., editors), Contemporary Mathematics Series, American Mathematical Socity, Providence, RI, 2004, pp. 37–59.Google Scholar
Felgner, U., Choice functions on sets and classes, Sets and Classes (Bernays, P., editor), Studies in Logic and the Foundations of Mathematics, vol. 84, North-Holland, Amsterdam, 1976, pp. 217–255.Google Scholar
Hamkins, J. D., Does ZFC prove the universe is linearly orderable? MathOverflow answer, 2012. Available at http://mathoverflow.net/q/110823.Google Scholar
Jockusch, C., Ramsey’s theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
Kaufmann, M., Blunt and topless end extensions of models of set theory, this Journal, vol. 48 (1983), pp. 1053–1073.Google Scholar
Kunen, K., Set theory, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland Publishing Co., Amsterdam, 1983.Google Scholar
Leshem, A., On the consistency of the definable tree property on ${\aleph _1}$, this Journal, vol. 65 (2000), pp. 1204–1214.Google Scholar
Mostowski, A., Some impredicatve definitions in the axiomatic set-theory. Fundamenta Mathematicae, vol. 37 (1950), pp. 111–124.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York, 1967.Google Scholar
Wang, H., Popular Lectures on Mathematical Logic, Dover Publications, Mineola, 1993.Google Scholar