Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T21:45:25.935Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak cardinality theorems†

Published online by Cambridge University Press:  12 March 2014

Till Tantau
Till Tantau*
Affiliation:
Fakultät für Elektrotechnik und Informatik, Technische Universität Berlin, Berlin, GermanyE-mail:, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kummer's Cardinality Theorem states that a language A must be recursive if a Turing machine can exclude for any n words 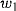, …, one of the n + 1 possibilities for the cardinality of {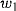, …, }⋂ A. There was good reason to believe that this theorem is a peculiarity of recursion theory: neither the Cardinality Theorem nor weak forms of it hold for resource-bounded computational models like polynomial time. This belief may be flawed. In this paper it is shown that weak cardinality theorems hold for finite automata and also for other models. An explanation is proposed as to why recursion-theoretic and automata-theoretic weak cardinality theorems hold, but not corresponding 'middle-ground theorems': The recursion- and automata-theoretic weak cardinality theorems are instantiations of purely logical weak cardinality theorems. The logical theorems can be instantiated for logical structures characterizing recursive computations and finite automata computations. A corresponding structure characterizing polynomial time computations does not exist.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 70 , Issue 3 , September 2005 , pp. 861 - 878
Copyright
Copyright © Association for Symbolic Logic 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

An earlier version of this paper was presented at the FCT 2003 conference [Tantau, 2003b].

References

REFERENCES

[2003]Austinat, Holger, Diekert, Volker, and Hertrampf, Ulrich, A structural property of regular frequency computations, Theoretical Computer Science, vol. 292 (2003), no. 1, pp. 33–43.CrossRefGoogle Scholar
[2000]Austinat, Holger, Diekert, Volker, Hertrampf, Ulrich, and Petersen, Holger, Regular frequency computations, Proceedings of the RIMS symposium on algebraic systems, formal languages and computation, RIMS Kokyuroku, vol. 1166, Research Institute for Mathematical Sciences, Kyoto University, Japan, 2000, pp. 35–42.Google Scholar
[1987]Beigel, Richard, Query-limited reducibilities, Ph.D. thesis, Stanford University, USA, 1987.Google Scholar
[2000]Beigel, Richard, Gasarch, William I., Kummer, Martin, Martin, Georgia, Mc-Nicholl, Timothy, and Stephan, Frank, The complexity of , this Journal, vol. 65 (2000), no. 1, pp. 1–18.Google Scholar
[1962]Buchi, Julius Richard, On a decision method in restricted second-order arithmetic, Proceedings of the 1960 international congress on logic, methodology and philosophy of science, Stanford University Press, 1962, pp. 1–11.Google Scholar
[1989]Cai, Jin-Yi and Hemachandra, Lane A., Enumerative counting is hard, Information and Computation, vol. 82 (1989), no. 1, pp. 34–44.CrossRefGoogle Scholar
[1991]Gasarch, William I., Bounded queries in recursion theory: A survey, Proceedings of the 6th structure in complexity theory conference, IEEE Computer Society Press, 1991, pp. 62–78.Google Scholar
[1999]Gasarch, William I. and Martin, Georgia A., Bounded queries in recursion theory, Progress in Computer Science and Applied Logic, vol. 16, Birkhäuser, 1999.CrossRefGoogle Scholar
[1992]Harizanov, Valentina, Kummer, Martin, and Owings, Jim, Frequency computations and the cardinality theorem, this Journal, vol. 52 (1992), no. 2, pp. 682–687.Google Scholar
[1989]Hemachandra, Lane A., The strong exponential hierarchy collapses, Journal of Computer and System Sciences, vol. 39 (1989), no. 3, pp. 299–322.CrossRefGoogle Scholar
[1998]Hemaspaandra, Edith, Hemaspaandra, Lane, and Hempel, Harald, A downward collapse in the polynomial hierarchy, SIAM Journal on Computing, vol. 28 (1998), no. 2, pp. 383–393.CrossRefGoogle Scholar
[1993]Hoene, Albrecht and Nickelsen, Arfst, Counting, selecting, and sorting by query-bounded machines, Proceedings of the 10th international symposium on theoretical aspects of computer science, Lecture Notes in Computer Science, vol. 665, Springer-Verlag, 1993, pp. 196–205.Google Scholar
[1988]Immerman, Neil, Nondeterministic space is closed under complementation, SIAM Journal on Computing, vol. 17 (1988), no. 5, pp. 935–938.CrossRefGoogle Scholar
[1989]Kadin, Jim, pNP[O(logn)] and sparse Turing-complete sets for NP, Journal of Computer and System Sciences, vol. 39 (1989), no. 3, pp. 282–298.CrossRefGoogle Scholar
[1976]Kinber, Efim B., Frequency computations infinite automata, Cybernetics, vol. 2 (1976), pp. 179–187.Google Scholar
[1992]Kummer, Martin, A proof of Beigel's cardinality conjecture, this Journal, vol. 57 (1992), no. 2, pp. 677–681.Google Scholar
[1994]Kummer, Martin and Stephan, Frank, Effecitive search problems, Mathematical Logic Quarterly, vol. 40 (1994), no. 2, pp. 224–236.CrossRefGoogle Scholar
[1982]Mahaney, Stephen R., Sparse complete sets for NP: Solution of a conjecture of Berman and Hartmanis, Journal of Computer and System Sciences, vol. 25 (1982), no. 2, pp. 130–143.CrossRefGoogle Scholar
[1963]McNaughton, Richard, Review of [Büchi, 1962], this Journal, vol. 28 (1963), no. 1, pp. 100–102.Google Scholar
[1997]Nickelsen, Arfst, On polynomially D-verbose sets, Proceedings of the 14th international symposium on theoretical aspects of computer science, Lecture Notes in Computer Science, vol. 1200, Springer-Verlag, 1997, pp. 307–318.Google Scholar
[2001]Nickelsen, Arfst, Polynomial time partial information classes, Wissenschaft und Technik Verlag, 2001, Dissertation, Technical University of Berlin, 1999.Google Scholar
[1989]Owings, James C. Jr., A cardinality version of Beigel's nonspeedup theorem, this Journal, vol. 54 (1989), no. 3, pp. 761–767.Google Scholar
[1994]Papadimitriou, Christos H., Computational complexity, Addison-Wesley, 1994.Google Scholar
[1946]Quine, Willard von Orman, Concatenation as a basis for arithmetic, this Journal, vol. 11 (1946), no. 4, pp. 104–114.Google Scholar
[1967]Shoenfdild, Joseph R., Mathematical logic, Association for Symbolic Logic, 1967.Google Scholar
[1994]Straubing, Howard, Finite automata, formal logic, and circuit complexity, Progress in Theoretical Computer Science, Birkhäuser, 1994.CrossRefGoogle Scholar
[1988]Szelepcsényi, Robert, The method of forced enumeration for nondeterministic automata, Acta lnformatica, vol. 23 (1988), no. 3, pp. 279–284.CrossRefGoogle Scholar
[2003a]Tantau, Till, On structural similarities of finite automata and Turing machine enumerability classes, Wissenschaft und Technik Verlag, 2003, Dissertation, Technical University of Berlin, 2003.Google Scholar
[2003b]Tantau, Till, Weak cardinality theorems for first-order logic, Proceedings of the 14th symposium on fundamentals of computation theory (Lingas, Andrzej and Nilsson, Bengt J., editors), Lecture Notes in Computer Science, vol. 2751, Springer-Verlag, 2003, pp. 400–411.CrossRefGoogle Scholar
[2004]Tantau, Till, Comparing verboseness for finite automata and Turing machines, Theory of Computing Systems, vol. 37 (2004), no, 1, pp. 95–109.CrossRefGoogle Scholar
[1963]Trakhtenbrot, Boris A., On the frequency computation of functions, Algebra i Logika, vol. 2 (1963), pp. 25–32, In Russian.Google Scholar