Article contents
WAYS OF DESTRUCTION
Published online by Cambridge University Press: 08 October 2021
Abstract
We study the following natural strong variant of destroying Borel ideals: 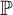 $\mathbb {P}$
$\mathbb {P}$
 $+$
-destroys
$+$
-destroys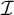 $\mathcal {I}$
if
$\mathcal {I}$
if 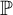 $\mathbb {P}$
adds an
$\mathbb {P}$
adds an 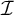 $\mathcal {I}$
-positive set which has finite intersection with every
$\mathcal {I}$
-positive set which has finite intersection with every 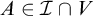 $A\in \mathcal {I}\cap V$
. Also, we discuss the associated variants
$A\in \mathcal {I}\cap V$
. Also, we discuss the associated variants 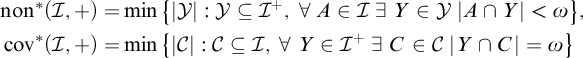 $$ \begin{align*} \mathrm{non}^*(\mathcal{I},+)=&\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^+,\; \forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\},\\ \mathrm{cov}^*(\mathcal{I},+)=&\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\; \forall\;Y\in\mathcal{I}^+\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\} \end{align*} $$
$$ \begin{align*} \mathrm{non}^*(\mathcal{I},+)=&\min\big\{|\mathcal{Y}|:\mathcal{Y}\subseteq\mathcal{I}^+,\; \forall\;A\in\mathcal{I}\;\exists\;Y\in\mathcal{Y}\;|A\cap Y|<\omega\big\},\\ \mathrm{cov}^*(\mathcal{I},+)=&\min\big\{|\mathcal{C}|:\mathcal{C}\subseteq\mathcal{I},\; \forall\;Y\in\mathcal{I}^+\;\exists\;C\in\mathcal{C}\;|Y\cap C|=\omega\big\} \end{align*} $$
Among other results, (1) we give a simple combinatorial characterisation when a real forcing 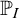 $\mathbb {P}_I$
can
$\mathbb {P}_I$
can  $+$
-destroy a Borel ideal
$+$
-destroy a Borel ideal 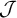 $\mathcal {J}$
; (2) we discuss many classical examples of Borel ideals, their
$\mathcal {J}$
; (2) we discuss many classical examples of Borel ideals, their  $+$
-destructibility, and cardinal invariants; (3) we show that the Mathias–Prikry,
$+$
-destructibility, and cardinal invariants; (3) we show that the Mathias–Prikry, 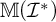 $\mathbb {M}(\mathcal {I}^*)$
-generic real
$\mathbb {M}(\mathcal {I}^*)$
-generic real  $+$
-destroys
$+$
-destroys 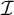 $\mathcal {I}$
iff
$\mathcal {I}$
iff 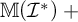 $\mathbb {M}(\mathcal {I}^*)\ +$
-destroys
$\mathbb {M}(\mathcal {I}^*)\ +$
-destroys 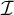 $\mathcal {I}$
iff
$\mathcal {I}$
iff 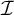 $\mathcal {I}$
can be
$\mathcal {I}$
can be  $+$
-destroyed iff
$+$
-destroyed iff 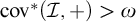 $\mathrm {cov}^*(\mathcal {I},+)>\omega $
; (4) we characterise when the Laver–Prikry,
$\mathrm {cov}^*(\mathcal {I},+)>\omega $
; (4) we characterise when the Laver–Prikry, 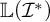 $\mathbb {L}(\mathcal {I}^*)$
-generic real
$\mathbb {L}(\mathcal {I}^*)$
-generic real  $+$
-destroys
$+$
-destroys 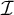 $\mathcal {I}$
, and in the case of P-ideals, when exactly
$\mathcal {I}$
, and in the case of P-ideals, when exactly 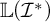 $\mathbb {L}(\mathcal {I}^*)$
$\mathbb {L}(\mathcal {I}^*)$
 $+$
-destroys
$+$
-destroys 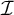 $\mathcal {I}$
; and (5) we briefly discuss an even stronger form of destroying ideals closely related to the additivity of the null ideal.
$\mathcal {I}$
; and (5) we briefly discuss an even stronger form of destroying ideals closely related to the additivity of the null ideal.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 3
- Cited by



