Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:53:39.051Z Has data issue: false hasContentIssue false
  • English
  • Français

VARSOVIAN MODELS I

Published online by Cambridge University Press:  01 August 2018

GRIGOR SARGSYAN  and
RALF SCHINDLER
GRIGOR SARGSYAN
Affiliation:
DEPARTMENT OF MATHEMATICS RUTGERS UNIVERSITY NEW BRUNSWICK, NJ 08901, USAE-mail:[email protected]
RALF SCHINDLER
Affiliation:
INSTITUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG WWU MÜNSTER MÜNSTER, GERMANYE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Msw denote the least iterable inner model with a strong cardinal above a Woodin cardinal. By [11], Msw has a fully iterable core model, 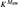${K^{{M_{{\rm{sw}}}}}}$, and Msw is thus the least iterable extender model which has an iterable core model with a Woodin cardinal. In V, 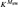${K^{{M_{{\rm{sw}}}}}}$ is an iterate of Msw via its iteration strategy Σ.

We here show that Msw has a bedrock which arises from 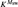${K^{{M_{{\rm{sw}}}}}}$ by telling 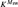${K^{{M_{{\rm{sw}}}}}}$ a specific fragment ${\rm{\bar{\Sigma }}}$ of its own iteration strategy, which in turn is a tail of Σ. Hence Msw is a generic extension of 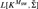$L[{K^{{M_{{\rm{sw}}}}}},{\rm{\bar{\Sigma }}}]$, but the latter model is not a generic extension of any inner model properly contained in it.

These results generalize to models of the form Ms (x) for a cone of reals x, where Ms (x) denotes the least iterable inner model with a strong cardinal containing x. In particular, the least iterable inner model with a strong cardinal above two (or seven, or boundedly many) Woodin cardinals has a 2-small core model K with a Woodin cardinal and its bedrock is again of the form 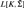$L[K,{\rm{\bar{\Sigma }}}]$.

Keywords

03E1503E4503E60mouseinner model theorydescriptive set theoryhod mouse
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 496 - 528
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bukovský, L., Characterization of generic extensions of models of set theory. Fundamenta Mathematica, vol. 83 (1973), pp. 35–46.CrossRefGoogle Scholar
Fuchs, G., Hamkins, J., and Reitz, J., Set-theoretic geology. Annals of Pure and Applied Logic, vol. 166 (2015), pp. 464–501.CrossRefGoogle Scholar
Fuchs, G. and Schindler, R., Inner model theoretic geology, this Journal, vol. 81 (2016), pp. 972–996.Google Scholar
Jensen, R. B., The core model for non–overlapping extender sequences, handwritten notes.Google Scholar
Jensen, R., Schimmerling, E., Schindler, R., and Steel, J., Stacking mice, this Journal, vol. 74 (2009), pp. 315–335.Google Scholar
Koellner, P. and Woodin, W. H., Large cardinals from determinacy, Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamori, A., editors), Springer–Verlag, Berlin, 2010, pp. 1951–2120.CrossRefGoogle Scholar
Mitchell, W. and Schindler, R., A universal extender model without large cardinals in V, this Journal, vol. 69 (2004), pp. 371–386.Google Scholar
Mitchell, W. and Steel, J. R., Fine Structure and Iteration Trees, Lecture Notes in Logic, vol. 3, Springer-Verlag, Berlin, 1994.CrossRefGoogle Scholar
Sargsyan, G., Hod mice and the Mouse Set Conjecture, Memoirs of the American Mathematical Society, vol. 236, no. 1111.Google Scholar
Sargsyan, G., Schindler, R., and Schlutzenberg, F., Varsovian models II, in preparation.Google Scholar
Sargsyan, G. and Zeman, M., in preparation.Google Scholar
Schindler, R., Set Theory: Exploring Independence and Truth, Springer–Verlag, Berlin, 2014.CrossRefGoogle Scholar
Schindler, R., The long extender algebra. Archive for Mathematical Logic, vol. 57 (2018), no. 1–2, pp. 73–82.CrossRefGoogle Scholar
Schindler, R., Steel, J. R., and Zeman, M., Deconstructing inner model theory, this Journal, vol. 67 (2002), pp. 721–736.Google Scholar
Schindler, R. and Steel, J., The self-iterability of L[E], this Journal, vol. 74 (2009), pp. 751–779.Google Scholar
Schlutzenberg, F., Iterability for stacks, preprint, 2015.Google Scholar
Schlutzenberg, F. and Steel, J., Normalizing iteration trees, in preparation.Google Scholar
Steel, J., The Core Model Iterability Problem, Lecture Notes in Logic, vol. 8, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Steel, J., An outline of inner model theory, Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamori, A., editors), Springer–Verlag, Berlin, 2010, pp. 1595–1684.CrossRefGoogle Scholar
Steel, J., Normalizing iteration trees and comparing iteration strategies, preprint, available at https://math.berkeley.edu/∼steel/papers/strategycompare.jan2018.pdf.Google Scholar
Steel, J. and Woodin, W. H., HOD as a core model, Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. III (Kechris, A., Lwe, B., and Steel, J., editors), Lecture Notes in Logic, Cambridge University Press, 2016, pp. 257–346.CrossRefGoogle Scholar
Usuba, T., The downward directed grounds hypothesis and very large cardinals.Journal of Mathematical Logic, 2017, to appear.CrossRefGoogle Scholar
Woodin, W. H., private communication, June 2009.Google Scholar