Article contents
The upper semilattice of degrees ≤ 0′ is complemented
Published online by Cambridge University Press: 12 March 2014
Extract
Let 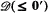 denote the set of degrees ≤ 0′. A degree a ≤ 0′ is said to be complemented in
denote the set of degrees ≤ 0′. A degree a ≤ 0′ is said to be complemented in 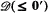 if there exists a degree b ≤ 0′ such that b ∪ a = 0′ and b ∩ a = 0. R.W. Robinson (cf. [11]) showed that every degree a ≤ 0′ satisfying a″ = 0″ is complemented in
if there exists a degree b ≤ 0′ such that b ∪ a = 0′ and b ∩ a = 0. R.W. Robinson (cf. [11]) showed that every degree a ≤ 0′ satisfying a″ = 0″ is complemented in 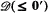 and the author [8] showed that every degree a ≤ 0′ satisfying a′ = 0″ is complemented in
and the author [8] showed that every degree a ≤ 0′ satisfying a′ = 0″ is complemented in 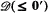 . Also, in [2], R. L. Epstein showed that every r.e. degree is complemented in
. Also, in [2], R. L. Epstein showed that every r.e. degree is complemented in 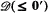 . In this paper we will show that in fact every degree ≤ 0′ is complemented in
. In this paper we will show that in fact every degree ≤ 0′ is complemented in 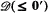 . We will further show that the same is true in the upper semilattice of degrees ≤ c, where c is any complete degree. This is in contrast to the situation in the upper semilattice of r.e. degrees in which, as Lachlan [6] has shown, no degree other than 0 and 0′ is complemented.
. We will further show that the same is true in the upper semilattice of degrees ≤ c, where c is any complete degree. This is in contrast to the situation in the upper semilattice of r.e. degrees in which, as Lachlan [6] has shown, no degree other than 0 and 0′ is complemented.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 15
- Cited by


