Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:37:31.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Universal sets for pointsets properly on the nth level of the projective hierarchy

Published online by Cambridge University Press:  12 March 2014

Greg Hjorth ,
Leigh Humphries  and
Arnold W. Miller
Greg Hjorth
Affiliation:
Department of Mathematics & Statistics, The University of Melbourne, Parkville, Victoria 3010, Australia, URL: www.math.ucla.edu/~greg, E-mail: [email protected]
Arnold W. Miller
Affiliation:
University of Wisconsin-Madison, Department of Mathematics, Van Vleck Hall, 480 Lincoln Drive, Madison, Wisconsin 53706-1388, USA, E-mail: [email protected] URL: http://www.math.wisc.edu/~miller
Get access Rights & Permissions [Opens in a new window]

Abstract

The Axiom of Projective Determinacy implies the existence of a universal 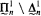set for every n ≥ 1. Assuming 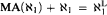there exists a universal 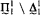set. In ZFC there is a universal 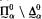set for every α.

Keywords

Universal setsProjective DetermancyWadge reducibilityConstructible UniverseMartin's Axiom
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 1 , March 2013 , pp. 237 - 244
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, K. J., Gandy, R. O., and Moschovakis, Y. N., The next admissible set, this Journal, vol. 36 (1971), pp. 108–120.Google Scholar
[2]Fremlin, D. H., Consequences of Martin's axiom, Cambridge Tracts in Mathematics, 84, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
[3]Harrington, Leo, Long projective wellorderings, Annul of Mathematical Logic, vol. 12 (1977), no. 1, pp. 1–24.CrossRefGoogle Scholar
[4]Hjorth, Greg, Universal co-analytic sets, Proceedings of the American Mathematical Society, vol. 124 (1996), no. 12, pp. 3867–3873.CrossRefGoogle Scholar
[5]Jech, T., Set theory, Springer, 2003.Google Scholar
[6]Kanamori, Akihiro, The higher infinite. Large cardinals in set theory from their beginnings, Perspectives in Mathematical Logic, Springer, 1994.Google Scholar
[7]Kechris, Alexander S., The theory of countable analytical sets, Transactions of the American Mathematical Society, vol. 202 (1975), pp. 259–297.CrossRefGoogle Scholar
[8]Kechris, Alexander S., Classical descriptive set theory, Graduate Texts in Mathematics, 156, Springer, 1995.CrossRefGoogle Scholar
[9]Kunen, Kenneth, Set theory. An introduction to independence proofs, Studies in Logic and the Foundations of Mathematics, vol. 102, North-Holland, 1983, reprint of the 1980 original.Google Scholar
[10]Mansfield, R. and Weitkamp, G., Recursive uspects of descriptive set theory, Oxford University Press, 1985.Google Scholar
[11]Martin, Donald A., Borel determinacy, Annals of Mathematics, Series 2, vol. 102 (1975), no. 2, pp. 363–371.CrossRefGoogle Scholar
[12]Martin, Donald A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), no. 2, pp. 143–178.CrossRefGoogle Scholar
[13]Miller, Arnold W., Some interesting problems, http://www.math.wisc.edu/~miller/res/problem.pdf.Google Scholar
[14]Moschovakis, Y. N., Descriptive set theory, North-Holland, 1980.Google Scholar
[15]Rudin, M. E., Martin's axiom, Handbook of mathematical logic (Barwise, Jon, editor), Studies in Logic and the Foundations of Mathematics, vol. 90, North-Holland, 1977, pp. 419–502.CrossRefGoogle Scholar
[16]Sacks, G., Higher recursion theory, Springer, 1990.CrossRefGoogle Scholar
[17]Steel, J. R., Analytic sets and borel isomorphisms, Fundamenta Mathematica, vol. 108 (1980), no. 2, pp. 83–88.CrossRefGoogle Scholar