Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Komjáth, Péter
Larson, Jean A.
and
Sauer, Norbert
2011.
The quasi order of graphs on an ordinal.
Discrete Mathematics,
Vol. 311,
Issue. 15,
p.
1451.
Hrušák, Michael
2014.
Recent Progress in General Topology III.
p.
601.
Baldwin, John T.
and
Larson, Paul B.
2016.
Iterated elementary embeddings and the model theory of infinitary logic.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 3,
p.
309.
Cody, Brent
and
Eskew, Monroe
2018.
Rigid ideals.
Israel Journal of Mathematics,
Vol. 224,
Issue. 1,
p.
343.
Eskew, Monroe
2019.
More rigid ideals.
Israel Journal of Mathematics,
Vol. 233,
Issue. 1,
p.
225.


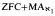 , then for every real
, then for every real 