Une théorie de Galois imaginaire

Extract

La communauté mathématique doit être reconnaissante à Saharon Shelah pour une invention d'une ingénieuse simplicité, celle d'avoir associé à chaque structure M une structure M^eq comprenant, outre les éléments de M, des “éléments imaginaires” qui sont virtuellement présents dans M. La finalité de cette construction est de pourvoir toute formule 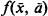à paramètres dans M, et même dans M^eq, d'un ensemble de définition minimum; tout cela est rappelé dans la première section du présent article.

On peut a priori douter de l'utilité d'une construction si innocente, dont la propriété fondamentale est pratiquement évidente; et pourtant elle a été abondamment montrée par son auteur, à qui elle a permis, dans les théorèmes de classification des modèles, une décomposition des types en éléments simples, qu'on ne voit pas dans M.

Cette construction d'un plus petit ensemble de définition pour une formule en rappelle une autre, qui est bien connue des algébristes, celle du corps de définition d'un idéal. Et comme la théorie des corps algébriquement clos de caractéristique donnée élimine les quanteurs, on a le sentiment que l'adjonction d'imaginaires aux modèles de cette théorie est inutile, en un mot qu'elle “élimine les imaginaires”; pour vérifier le bien-fondé de ce sentiment, il convient d'abord de préciser ce qu'on entend par là, ce qui est fait dans la deuxième section.