Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-16T11:15:02.582Z Has data issue: false hasContentIssue false
  • English
  • Français

Undecidable wreath products and skew power series fields

Published online by Cambridge University Press:  12 March 2014

Françoise Delon  and
Patrick Simonetta
Françoise Delon
Affiliation:
Équipe de Logique Mathématique de Paris VII, 2, Place Jussieu—Case 7012, 75251 Paris Cedex 05, France, E-mail: [email protected]
Patrick Simonetta
Affiliation:
Équipe de Logique Mathématique de Paris VII, 2, Place Jussieu—Case 7012, 75251 Paris Cedex 05, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We prove the undecidability of a very large class of restricted and unrestricted wreath products (Theorem 1.2), and of some skew fields of power series (Section2). Both undecidabilities are obtained by interpreting some enrichments of twisted wreath products, which are themselves proved to be undecidable (Proposition 1.1).

We consider division rings of power series in various languages:

We show (Theorem 2.8) that every power series division ring k((B)), whose field of constants k is commutative and whose ordered group of exponents is noncommutative with a convex center, is undecidable in every extension of the language of rings where the valuation and the ordered group B are definable.

For certain k and B we prove here the undecidability of the structure

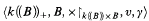
where X↾k((B))xB is the restriction of the multiplication to k((B)) Χ B,and γ is a given conjugation of k((B)). This shows that we cannot hope to improve our previous result, a sort of Ax-Kochen-Ershov principle for power series division rings, which ensures that

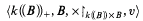
is decidable for every decidable solvable B.

Keywords

undecidable groupsundecidable fieldswreath productspower series division rings
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 1 , March 1998 , pp. 237 - 246
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ax, J., On the undecidability of power series fields, Proceedings of the American Mathematical Society, vol. 16 (1965), p. 846.Google Scholar
[2]Delon, F., Q muni de l'arithmetique faible de Penzin est décidable, to appear in Proceedings of the American Mathematical Society.Google Scholar
[3]Delon, F. and Rouani, Y., Indécidabilité de corps de séries formelles, this Journal, vol. 53 (1988), pp. 1227–1235.Google Scholar
[4]Delon, F. and Simonetta, P., Un principe d' Ax-Kochen-Ershov pour des structures intérmedials entre groupes et corps valués, to appear in this Journal.Google Scholar
[5]Neumann, B. H., On ordered division rings, Transactions of the American Mathematical Society vol. 66 (1949), pp. 202–252.CrossRefGoogle Scholar
[6]Neumann, B. H., On ordered groups, American Journal of Mathematics vol. 71 (1949), pp. 1–18.CrossRefGoogle Scholar
[7]Neumann, B. H., Twisted wreath products of groups, Archiv der Mathematik vol. 17 (1963), pp. 1–6.CrossRefGoogle Scholar
[8]Robinson, J., The decision problem for fields, Symposium on the theory of models, North-Holland, Amsterdam, 1965, pp. 299–311.Google Scholar
[9]Robinson, R., Undecidable rings, Transactions of the American Mathematical Society vol. 70 (1951), pp. 137–159.CrossRefGoogle Scholar
[10]Simonetta, P., Décidabilité et interprétabilité dans les corps et les groupes non commutatifs, Thése, Université Paris 7, 1994.Google Scholar