Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T07:30:17.456Z Has data issue: false hasContentIssue false
  • English
  • Français

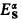Undecidable complexity statements in -arithmetic

Published online by Cambridge University Press:  12 March 2014

Ron Sigal
Ron Sigal*
Affiliation:
Department of Computer and Information Science, Brooklyn College, Brooklyn, New York 11210
*
Dipartimento di Matematica, Università di Catania, 95125 Catania, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

The failure of a large and diverse body of work to settle some of the now-classical questions of computational complexity (notably P =? NP) suggests that they might not, in fact, be resolvable by established proof techniques.

Hartmanis and Hopcroft [HH] raised the issue of independent statements about computational complexity in 1976, constructing, for any consistent r.e. theory T capable of expressing statements about Turing machines, a Turing machine MT such that statements which intuitively express the computational complexity of MT are independent of T. Their technique involves a simple diagonalizing search over the theorems of T. In this paper we prove a constructive version of their independence result in the context of a generalization of a hierarchy of free variable logics defined by Rose [R1]. These logics are based on an axiomatized treatment of an extension by Löb and Wainer [LW] of Grzegorczyk's [G] hierarchy into the transfinite. Associated with each extended Grzegorczyk class 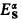(relative to an ordinal notation system S satisfying certain conditions) is the logic 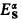-arithmetic.

Free variable logics are interesting from the perspective of theoretical computer science. We may construe the equational definition of functions as a form of programming system. Each 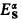-arithmetic, then, has the nice property of containing both a programming system and a logic for stating and proving facts about programs.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 415 - 427
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Backus, J., Can programming be liberated from the von Neumann style? A functional style and its algebra of programs, Communications of the Association for Computing Machinery, vol. 21 (1978), pp. 613–641.CrossRefGoogle Scholar
[G]Grzegorczyk, A., Some classes of recursive functions, Dissertationes Mathematicae Rozprawy Matematyczne, vol. 4 (1953).Google Scholar
[HH]Hartmanis, J. and Hopcroft, J. E., Independence results in computer science, ACM SIGACT News, vol. 8 (1976), no. 4, pp. 13–24.CrossRefGoogle Scholar
[HWW]Halpern, J., Williams, J., and Wimmers, E., Completion of rewrite rules and rewrite strategies for FP, IBM Research report RJ5099, 1986.Google Scholar
[K]Kleene, S. C., Extension of an effectively generated class of functions by enumeration, Colloquium Mathematicum, vol. 6 (1958), pp. 67–78.CrossRefGoogle Scholar
[LW]Löb, M. H. and Wainer, S. S., Hierarchies of number-theoretic functions. I, II, and Correction, Archiv für Mathematische Logik und Grundlagenforschung, vol. 13 (1970), pp. 39–51, 97–113; vol. 14 (1971), pp. 198–199.CrossRefGoogle Scholar
[R1]Rose, H. E., Eα-arithmetic and transfinite induction, this Journal, vol. 37 (1972), pp. 19–30.Google Scholar
[R2]Rose, H. E., Subrecursion: functions and hierarchies, Oxford University Press, Oxford, 1984.Google Scholar
[R3]Rose, H. E., personal communication.Google Scholar
[Sc1]Schmidt, D., Built-up systems of fundamental sequences and hierarchies of number-theoretic functions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 18 (1976/1977), pp. 47–53.CrossRefGoogle Scholar
[Sc2]Schmidt, D., Postscript to [Sc1], Archiv für Mathematische Logik und Grundlagenforschung, vol. 18 (1976/1977), pp. 145–146.CrossRefGoogle Scholar
[Si1]Sigal, R., Undecidable complexity statements in a hierarchy of extensions of primitive recursive arithmetic, Ph.D. thesis, New York University, New York, 1983.Google Scholar
[Si2]Sigal, R., Undecidable complexity statements in a hierarchy of extensions of primitive recursive arithmetic, Technical Report TR-24–87, Department of Computer and Information Science, Brooklyn College, Brooklyn, New York, 1987.Google Scholar
[T]Tait, W. W., Nested recursion, Mathematische Annalen, vol. 143 (1961), pp. 236–250.CrossRefGoogle Scholar
[Ze]Zemke, F.P.r.-regulated systems of notation and the subrecursive hierarchy equivalence property, Transactions of the American Mathematical Society, vol. 234 (1977), pp. 89–118.CrossRefGoogle Scholar