Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T20:12:33.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Uncountable master codes and the jump hierarchy

Published online by Cambridge University Press:  12 March 2014

Robert S. Lubarsky
Robert S. Lubarsky*
Affiliation:
Department of Mathematics, Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Extract

The Turing jump can easily be iterated any finite number of times. The challenge is posed by by transfinite iterations. a(ω) has an intuitively compelling definition: {‹m, n›: n ∈ a(m)}. Starting with Putnam et al. [1], [2], [9] and culminating in Jockusch-Simpson [8] and Hodes [6], recent work has justified this ω-jump and extended it through .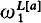

Of great use are the master codes of Jensen [3], [7]. Briefly, a Δn(Lβ)-master code is a complete Δn(Lβ) set of ordinals, with supremum as small as possible. Connections with classical recursion theory are tight. When the Δn(Lβ) master codes are reals, they are Turing equivalent. If a is a Δn(Lβ) MC, then a′ is a Δn + 1(Lβ) MC. Intuitively satisfying transfinite jumps, such as the ω-jump above, produce a Turing jump hierarchy equal to an initial segment of the master codes.

Hodes capitalized on these facts by defining 0α, α < 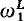, set-theoretically as the degree of the αth MC which is a real, and then proving the equivalence of a jump-theoretic definition of 0α. The successor codes are jumps of their predecessors, and for a limit λ, 0λ is the minimum of a set of degrees associated with {0α: α: < λ}.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 4 , December 1987 , pp. 952 - 958
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[0]Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[1]Boolos, G. and Putnam, H., Degrees of unsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
[2]Boyd, R., Hensel, G., and Putnam, H., A recursion-theoretic characterization of the ramified analytical hierarchy, Transactions of the American Mathematical Society, vol. 141 (1969), pp. 47–62.CrossRefGoogle Scholar
[3]Devlin, K. J., Aspects of constructibility, Lecture Notes in Mathematics, vol. 354, Springer-Verlag, Berlin, 1973.CrossRefGoogle Scholar
[4]Friedman, S. D., Negative solutions of Post's problem. II, Annals of Mathematics, ser. 2, vol. 113 (1981), pp. 25–43.CrossRefGoogle Scholar
[5]Friedman, S. D., Uncountable admissibles. II: Compactness, Israel Journal of Mathematics, vol. 40 (1981), pp. 129–149.CrossRefGoogle Scholar
[6]Hodes, H., Jumping through the transfinite, this Journal, vol. 45 (1980), pp. 204–220.Google Scholar
[7]Jensen, R. B., The fine structure of the constructible hierarchy, Annals of Mathematical Logic, vol. 8 (1972), pp. 229–308.CrossRefGoogle Scholar
[8]Jockusch, C. and Simpson, S., A degree-theoretic characterization of the ramified analytical hierarchy, Annals of Mathematical Logic, vol. 10 (1976), pp. 1–32.CrossRefGoogle Scholar
[9]Leeds, S. and Putnam, H., An intrinsic characterization of the hierarchy of constructible sets of integers, Logic Colloquium '69, North-Holland, Amsterdam, 1971, pp. 311–350.CrossRefGoogle Scholar
[10]Marek, W. and Srebrny, M., Gaps in the constructible universe, Annals of Mathematical Logic, vol. 6 (1974), pp. 359–394.CrossRefGoogle Scholar
[11]Sacks, G., Forcing with perfect closed sets, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, 1971, pp. 331–355.CrossRefGoogle Scholar
[12]Steel, J., Forcing with tagged trees, Annals of Mathematical Logic, vol. 15 (1978), pp. 55–74.CrossRefGoogle Scholar