Article contents
Two theories with axioms built by means of pleonasms
Published online by Cambridge University Press: 12 March 2014
Extract
This paper contains examples T1 and T2 of theories which answer the following questions:
(1) Does there exist an essentially undecidable theory with a finite number of non-logical constants which contains a decidable, finitely axiomatizable subtheory?
(2) Does there exist an undecidable theory categorical in an infinite power which has a recursive set of axioms? (Cf. [2] and [3].)
The theory T1 represents a modification of a theory described by Myhill [7]. The common feature of theories T1 and T2 is that in both of them pleonasms are essential in the construction of the axioms.
Let T1 be a theory with identity = which contains one binary predicate R(x, y) and is based on the axioms A1, A2, A3, B1, B2, B3, B4, Cnm which follow.
A1: x = x. A2: x = y ⊃ y = x. A3: x = y ∧ y = z ⊃ x = z.
(Axioms of identity.)
B1: R(x, x). B2: R(x, y) ⊃ R(y, x). B3: R (x, y) ∧ R(y, z) ⊃ R(x, z).
(Axioms of equivalence.)
B4: x = y ⊃ [R(z, x) ≡ R(z,y)].
Let φn be the formula
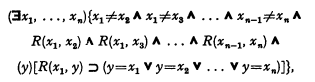
which express that there is an abstraction class of the relation R which has exactly n elements.
Let f(n) and g(n) be two recursive functions which enumerate two recursively inseparable sets [5], and call these sets X1 and X2.
We now specify the axioms Cmm.
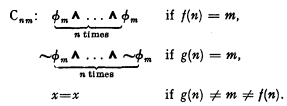
It is obvious that the set composed of the formulas A1−A3, B1−B4, Cnm (n,m = 1,2, …) is recursive.
The theory T1 is essentially undecidable; for if there were a complete and decidable extension T′1 (of it, then the recursive sets Z = {n: φn is provable in T′1} and Z′ = {n: ∼φn is provable in T′1} would separate the sets X1 and X2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1957
References
LITERATURE
- 4
- Cited by


