Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T21:33:54.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Two step iteration of almost disjoint families

Published online by Cambridge University Press:  12 March 2014

Jerry E. Vaughan
Jerry E. Vaughan*
Affiliation:
Department of Mathematical Sciences, University of North Carolina, at Greensboro, Greensboro, NC 27402, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Let E be an infinite set, and [E]ω the set of all countably infinite subsets of E. A family 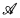⊂ [E]ω is said to be almost disjoint (respectively, pairwise disjoint) provided for A, B ∈ 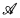, if A ≠ B then A ∩ B is finite (respectively, A ∩ B is empty). Moreover, an infinite family A is said to be a maximal almost disjoint family provided it is an infinite almost disjoint family not properly contained in any almost disjoint family. In this paper we are concerned with the following set of topological spaces defined from (maximal) almost disjoint families of infinite subsets of the natural numbers ω.

Keywords

almost disjoint familiessmall uncountable cardinalsiterations of ψHausdorffUrysohn
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 81 - 90
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Gilman, L. and Jerison, M., Rings of continuous functions, D. Van Nostrand Co. Inc., Princeton, 1960.Google Scholar
[2]Hechler, Stephen H., Short complete nested sequences in βN\N and small maximal almost-disjoint families, General Topology and its Applications, vol. 2 (1972), pp. 139–149.CrossRefGoogle Scholar
[3]Mrówka, S., On completely regular spaces, Fundamenta Mathematicae, vol. 41 (1954), pp. 105–106.Google Scholar
[4]Mrówka, S., Some set-theoretic constructions in topology, Fundamenta Mathematicae, vol. 94 (1977). no. 2, pp. 83–92.CrossRefGoogle Scholar
[5]Nyikos, P., Soukup, L., and Veličković, B., Hereditary normality of γN-spaces, Topology and its Applications, vol. 65 (1995), no. 1, pp. 9–19.Google Scholar
[6]Nyikos, Peter J. and Vaughan, Jerry E., The Scarborough-Stone problem for Hausdorff spaces, Topology and its Applications, vol. 44 (1992), no. 1–3, pp. 309–316.Google Scholar
[7]Scarborough, C. T. and Stone, A. H., Products of nearly compact spaces, Transactions of the Amererican Mathematical Society, vol. 124 (1966), pp. 131–147.CrossRefGoogle Scholar
[8]Shelah, S., Are and your cup of tea?, (publication number 700).Google Scholar
[9]Urysohn, P., Über die Mächtigkeit der zusammenhängenden Mengen, Mathematische Annalen vol. 94 (1925), pp. 262–295.Google Scholar
[10]van Douwen, E. K., The integers and topology, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 111–167.Google Scholar
[11]Vaughan, J. E., Products of perfectly normal, sequentially compact spaces, Journal of London Mathematical Society (2), vol. 14 (1976), pp. 517–520.CrossRefGoogle Scholar
[12]Vaughan, J. E., Small uncountable cardinals and topology, Open problems in topology (van Mill, J. and Reed, G. M., editors), North-Holland Publishing Co., Amsterdam, 1990, pp. 195–218.Google Scholar
[13]Vaughan, J. E., Almost disjoint families and iterations of Ψ. Abstracts of the American Mathematical Society, vol. 81 (1992), no. 874–54–102, p. 319.Google Scholar