Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T22:17:40.689Z Has data issue: false hasContentIssue false
  • English
  • Français

THE TUKEY ORDER ON COMPACT SUBSETS OF SEPARABLE METRIC SPACES

Published online by Cambridge University Press:  09 March 2016

PAUL GARTSIDE  and
ANA MAMATELASHVILI
PAUL GARTSIDE
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF PITTSBURGH PITTSBURGH, PA 15260, USAE-mail: [email protected]
ANA MAMATELASHVILI
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF PITTSBURGH PITTSBURGH, PA 15260, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

One partially ordered set, Q, is a Tukey quotient of another, P, if there is a map (a Tukey quotient) 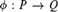$\phi :P \to Q$ carrying cofinal sets of P to cofinal sets of Q. Two partial orders which are mutual Tukey quotients of each other are said to be Tukey equivalent. Let 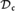${\cal D}_{\rm{}} $ be the partially ordered set of Tukey equivalence classes of directed sets of size 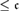$ \le {\rm{}}$. It is shown that 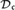${\cal D}_{\rm{}} $ contains an antichain of size 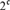$2^{\rm{}} $, and so has size 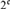$2^{\rm{}} $. The elements of the antichain are of the form 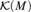${\cal K}\left( M \right)$, the set of compact subsets of a separable metrizable space M, ordered by inclusion. The order structure of such 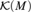${\cal K}\left( M \right)$’s under Tukey quotients is investigated. Relative Tukey quotients are introduced. Applications are given to function spaces and to the complexity of weakly countably determined Banach spaces and Gul’ko compacta.

Keywords

06A0754E35 (03E04, 54C35, 54D80)Partial orderTukey orderseparable metric spacecompact set
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 1 , March 2016 , pp. 181 - 200
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Argyros, S. A., Arvanitakis, A. and Mercourakis, S., Talagrand’s K σδproblem. Topology and its Applications, vol. 155 (2008), no. 15, pp. 1737–1755.CrossRefGoogle Scholar
Arkhangel’skii, A. V.. Topological Function Spaces. Mathematics and its Applications, vol. 78, Kluver Academic Publishers, Netherlands, 1992.Google Scholar
Avilés, A., Weakly countably determined spaces of high complexity. Studia Mathematica, vol. 185 (2008), pp. 291–303.Google Scholar
Baars, J., De Groot, J. and Pelant, J., Function Spaces of Completely Metrizable Spaces. Transactions of the American Mathematical Society, vol. 340 (1992), no. 2, pp. 871–883.CrossRefGoogle Scholar
Christensen, J. P. R., Topology and Borel Structure, North-Holland, Amsterdam-London; American Elsevier, New York, 1974.Google Scholar
Dobrinen, N. and Todorčević, S., Tukey types of ultrafilters. Illinois Journal of Mathematics, vol. 55 (2011), no. 3, pp. 907–951.CrossRefGoogle Scholar
Dobrinen, N. and Todorčević, S., A new class of Ramsey-classification theorems and their application in the Tukey theory of ultrafilters, Part 1. Transactions of the American Mathematical Society, vol. 366 (2013), no. 3, pp. 1659–1684.Google Scholar
Fremlin, D. H., Families of compact sets and Tukey’s ordering, Atti del Seminario Matematico e Fisico dell’Università di Modena, vol. 39 (1991), no. 1, pp. 29–50.Google Scholar
Fremlin, D. H., The partially ordered sets of measure theory and Tukey’s ordering. Note di Matematica, vol. 11 (1991), pp. 177–214.Google Scholar
Fremlin, D. H., Measure Theory, Volume 5, Torres Fremlin, Colchester, 2000.Google Scholar
Husek, M. and van Mill, J. (editors), Recent Progress in General Topology II, North-Holland, Amsterdam, 2002.Google Scholar
Isbell, J. R., Seven cofinal types. Journal of London Mathematical Society (2), vol. 4 (1972), pp. 394–416.Google Scholar
Knight, R. W. and McCluskey, A. E., ${\cal P}$(ℝ) ordered by homeomorphic embeddability, does not represent all posets of cardinality $2^{\rm{}} $. Topology and its Applications, vol. 156 (2009), pp. 1943–1945.Google Scholar
Louveau, A. and Velickovic, B., Analytic ideals and cofinal types. Annals of Pure and Applied Logic, vol. 99 (1999), pp. 171–195.Google Scholar
Mamatelashvili, A., Tukey Order on Sets of Compact Subsets of Topological Spaces, PhD thesis, http://d-scholarship.pitt.edu/21920/1/A.M._thesis_final_4.pdf.Google Scholar
Marciszewski, W. and Pelant, J., Absolute Borel Sets and Function Spaces. Transactions of the American Mathematical Society, vol. 349 (1997), no. 9, pp. 3585–3596.CrossRefGoogle Scholar
McCluskey, A. E., McMaster, T. B. M., and Watson, W. S.Representing set-inclusion by embeddability (among the subspaces of the real line). Topology and its Applications, vol. 96 (1999), pp. 89–92.Google Scholar
Milovich, D., Tukey classes of ultrafilters on ω. Topology Proceedings, vol. 32 (2008), pp. 351–362. Spring Topology and Dynamics Conference,Google Scholar
Moore, E. H. and Smith, H. L., A general theory of limits. American Journal of Mathematics, vol. 44 (1922), pp. 102–121.Google Scholar
Moore, J. T. and Solecki, S., A G δideal of compact sets strictly above the nowhere dense ideal in the Tukey order. Annals of Pure and Applied Logic, vol. 156 (2008), pp. 270–273.CrossRefGoogle Scholar
Raghavan, D. and Todorčević, S., Cofinal types of ultrafilters. Annals of Pure and Applied Logic, vol. 163 (2012), pp. 185–199.Google Scholar
Solecki, S. and Todorčević, S., Cofinal types of topological directed orders. Annales de l’Institut Fourier, Grenoble, vol. 54 (2004), no. 6, pp. 1877–1911.Google Scholar
Solecki, S. and Todorčević, S., Avoiding families and Tukey functions on the nowhere-dense ideal. Journal of the Institute of Mathematics of Jussieu, vol. 10 (2011), no. 2, pp. 405–435.Google Scholar
Talagrand, M., Espaces de Banach faiblement ${\cal K}$-analytiques. Annals of Mathematics (2), vol. 110 (1979), no. 3, pp. 407–438.CrossRefGoogle Scholar
Todorčević, S., Directed sets and cofinal types. Transactions of the American Mathemtical Society, vol. 290 (1985), no. 2, pp. 711–723.Google Scholar
Tukey, J. W., Convergence and unifomity in topology. Annals of Mathematics Studies, vol. 2, Princeton University Press, Princeton, 1940.Google Scholar
Vasak, L., On a generalization of weakly compactly generated spaces. Studia Mathematica, vol. 70 (1981), pp. 11–19.Google Scholar