Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T18:17:30.341Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSFINITE RECURSION IN HIGHER REVERSE MATHEMATICS

Published online by Cambridge University Press:  22 July 2015

NOAH SCHWEBER
NOAH SCHWEBER*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA, BERKELEY BERKELEY, CALIFORNIA 94720, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we investigate the reverse mathematics of higher-order analogues of the theory 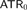$$ATR_0$$ within the framework of higher order reverse mathematics developed by Kohlenbach [11]. We define a theory 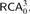$$RCA_0^3$$, a close higher-type analogue of the classical base theory 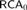$$RCA_0$$ which is essentially a conservative subtheory of Kohlenbach’s base theory 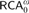$$RCA_{\rm{0}}^\omega$$. Working over 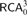$$RCA_0^3$$, we study higher-type analogues of statements classically equivalent to 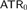$$ATR_0$$, including open and clopen determinacy, and examine the extent to which 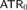$$ATR_0$$ remains robust at higher types. Our main result is the separation of open and clopen determinacy for reals, using a variant of Steel’s tagged tree forcing; in the presentation of this result, we develop a new, more flexible framework for Steel-type forcing.

Keywords

reverse mathematicshigher reverse mathematicsdeterminacyset theoryforcing
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 3 , September 2015 , pp. 940 - 969
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Friedman, Harvey, The analysis of mathematical texts, and their calibration in terms of intrinsic strength I, published on author’s website, 1975.Google Scholar
Friedman, Harvey, Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), vol. 1, pp. 235–242, Canadian Mathematical Congress, Montreal, Quebec, 1975.Google Scholar
Gandy, R. O., Computable functionals of finite type. I, Sets, Models and Recursion Theory Proceedings of the Summer School in Mathematical Logic and tenth Logic Colloquium(Leicester, 1965), pp. 202–242, North-Holland, Amsterdam, 1967.Google Scholar
Greenberg, Noam and Knight, Julia F., Computable structure theory using admissible recursion theory on ω1. Effective Mathematics of the Uncountable, Cambridge University Press, New York, 2013.CrossRefGoogle Scholar
Hachtman, Sherwood, Determinacy in third order arithmetic, submitted.Google Scholar
Harrison, Joseph, Recursive pseudo-well-orderings. Transactions of the American Mathematical Society, vol. 131(1968), pp. 526–543.CrossRefGoogle Scholar
Harnik, Victor, Set existence axioms for general (not necessarily countable) stability theory. Annals of Pure and Applied Logic, vol. 34 (1987), no. 3, pp. 231–243. Stability in model theory (Trento, 1984).CrossRefGoogle Scholar
Hunter, James, Higher-order reverse topology, ProQuest LLC, Ann Arbor, MI, 2008. Thesis (Ph.D.)–The University of Wisconsin - Madison.Google Scholar
Kechris, Alexander S., Classical descriptive set theory, vol. 156, Graduate Texts in Mathematics, Springer-Verlag, New York, 1995.Google Scholar
Kleene, S. C., Recursive functionals and quantifiers of finite types. I. Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
Kohlenbach, Ulrich, Higher order reverse mathematics, Reverse mathematics 2001, vol. 21, Lecture Notes in Logic, pp. 281–295, Association of Symbolic Logic, La Jolla, CA, 2005.Google Scholar
Kreuzer, Alexander P., Non-principal ultrafilters, program extraction and higher-order reverse mathematics. Journal of Mathematical Logic, vol. 12 (2012), no. 1, 1250002, p. 16.CrossRefGoogle Scholar
Kunen, Kenneth, Set theory, vol. 102, Studies in Logic and the Foundations of Mathematics, North-Holland, Amsterdam, 1983.Google Scholar
Longley, John R., Notions of computability at higher types. I, Logic Colloquium 2000, Lecture notes in Logic, vol.19, pp. 32–142, Association of Symbolic Logic, Urbana, IL, 2005.Google Scholar
Manzano, María, Extensions of first order logic, Cambridge Tracts in Theoretical Computer Science, vol. 19, Cambridge University Press, Cambridge, 1996.Google Scholar
Montalbán, Antonio, On the ${\rm{\Pi }}_1^1- $separation principle. MLQ Mathematical Logic Quarterly, vol. 54 (2008), no. 6, pp. 563–578.CrossRefGoogle Scholar
Moschovakis, Yiannis N., Hyperanalytic predicates. Transactions of the American Mathematical Society, vol. 129 (1967), pp. 249–282.CrossRefGoogle Scholar
Moschovakis, Yiannis N., Descriptive set theory, second edition, Mathematical Surveys and Monographs, vol. 155, American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Neeman, Itay, Necessary use of ${\rm{\Sigma }}_1^1$induction in a reversal, this Journal, vol. 76 (2011), no. 2, pp. 561–574.Google Scholar
Schweber, Noah, PhD thesis, University of California, Berkeley.Google Scholar
Shore, Richard A., Reverse mathematics, countable and uncountable: a computational approach, Effective Mathematics of the Uncountable, Cambridge University Press, New York, 2013.Google Scholar
Simpson, Stephen G., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1999.CrossRefGoogle Scholar
Steel, John R., Forcing with tagged trees. Annals of Mathematical Logic, vol. 15 (1978), no. 1, pp. 55–74.CrossRefGoogle Scholar
Sakamoto, Nobuyuki and Yamazaki, Takeshi, Uniform versions of some axioms of second order arithmetic.Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 587–593.CrossRefGoogle Scholar
Towsner, Henry, Ultrafilters in reverse mathematics, published in the ArXiv, 09 2011.Google Scholar
Bartel, L and van der, Waerden, Eine Bemerkung über die Unzerlegbarkeit von Polynomen. Mathematische Annalen,vol. 102 (1930), no. 1, pp. 738–739.Google Scholar