Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-18T08:09:22.490Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological properties of sets definable in weakly o-minimal structures

Published online by Cambridge University Press:  12 March 2014

Roman Wencel
Roman Wencel*
Affiliation:
Mathematical Institute, University of WrocławPl. Grunwaldzki 2/4, 50-384 Wrocław, Poland. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper is aimed at studying the topological dimension for sets definable in weakly o-minimal structures in order to prepare background for further investigation of groups, group actions and fields definable in the weakly o-minimal context. We prove that the topological dimension of a set definable in a weakly o-minimal structure is invariant under definable injective maps, strengthening an analogous result from [2] for sets and functions definable in models of weakly o-minimal theories. We pay special attention to large subsets of Cartesian products of definable sets, showing that if X, Y and S are non-empty definable sets and S is a large subset of X × Y. then for a large set of tuples 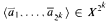, where k = dim(Y), the union of fibers 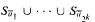is large in Y. Finally, given a weakly o-minimal structure 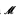, we find various conditions equivalent to the fact that the topological dimension in 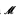enjoys the addition property.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 3 , September 2010 , pp. 841 - 867
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Arefiev, R., On monotonicity for weakly o-minimal structures, Algebra and model theory II (Pinus, A. G. and Ponomarev, A. N., editors), Novosibirsk, 1997, pp. 8–15.Google Scholar
[2]Macpherson, D., Marker, D., and Steinhorn, C., Weakly o-minimal structures and real closed fields, Transactions of the American Mathematical Society, vol. 352 (2000), pp. 5435–5483.CrossRefGoogle Scholar
[3]Pillay, A., On groups and fields definable in o-minimal structures, Journal of Pure and Applied Algebra, vol. 53 (1988), pp. 239–255.CrossRefGoogle Scholar
[4]van den Dries, L., Dimension of definable sets, algebraic boundedness and henselian fields, Annals of Pure and Applied Logic, vol. 45 (1989), pp. 189–209.CrossRefGoogle Scholar
[5]van den Dries, L., Tame topology and o-minimal structures, London Mathematical Society Lecture Notes Series, vol. 248, Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
[6]Verbovskiy, V.,Non-uniformly weakly o-minimal group, Algebra and model theory, 3 (Erlogol, 2001), Novosibirsk State Technical University, Novosibirsk, 2001, pp. 136–145 and 161.Google Scholar