Theories with finitely many models

Extract

If L is a first order language and n is a natural number, then L_n is the set of formulas which only make use of the variables x ₁,…,x_n . While every finite structure is determined up to isomorphism by its theory in L, the same is no longer true in L_n . This simple observation is the source of a number of intriguing questions. For example, Poizat [2] has asked whether a complete theory in L_n which has at least two nonisomorphic finite models must necessarily also have an infinite one. The purpose of this paper is to present some counterexamples to this conjecture.

Theorem. For each n ≤ 3 there are complete theories in L _2n−2 and L _2n−1 having exactly n + 1 models.

In our notation and definitions, we follow Poizat [2]. To test structures for elementary equivalence in L_n , we shall use the modified Ehrenfeucht-Fraïssé games of Immerman [1]. For convenience, we repeat his definition here.

Suppose that L is a purely relational language, each of the relations having arity at most n. Let 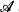and ℬ be two structures for L. Define the L_n game on 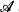and ℬ as follows. There are two players, I and II, and there are n pairs of counters a ₁, b ₁, …, a_n , b_n . On each move, player I picks up any of the counters and places it on an element of the appropriate structure.