Article contents
A theorem on deducibility for second-order functions1
Published online by Cambridge University Press: 12 March 2014
Extract
It is known that the usual definition of a dense series without extreme elements is complete with respect to first-order functions, in the sense that any first-order function on the base 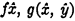 of a set of postulates defining such a series either is implied by the postulates or is inconsistent with them. It is here understood, in accordance with the usual convention, that when we speak of a function on the base
of a set of postulates defining such a series either is implied by the postulates or is inconsistent with them. It is here understood, in accordance with the usual convention, that when we speak of a function on the base 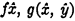 , the function shall be such as to place restrictions only upon elements belonging to the class determined by f; or, more exactly, every variable with a universal prefix shall occur under the hypothesis that its values satisfy f, while every variable with an existential prefix shall have this condition categorically imposed upon it.
, the function shall be such as to place restrictions only upon elements belonging to the class determined by f; or, more exactly, every variable with a universal prefix shall occur under the hypothesis that its values satisfy f, while every variable with an existential prefix shall have this condition categorically imposed upon it.
Consider a set of postulates defining a dense series without extreme elements, and add to this set the condition of Dedekind section, to be formulated as follows. Let the conjunction of the three functions,
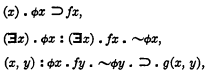
be written H(ϕ), where the free variables f and g, being parameters throughout, are suppressed. This is the hypothesis of Dedekind's condition, and the conclusion is
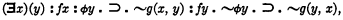
which may be written C(ϕ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1939
Footnotes
See abstract in this Journal, vol. 3 (1938), p. 59, or Bulletin of the American Mathematical Society, vol. 44 (1938), p. 36.
References
2 See Lewis, and Langford, , Symbolic logic, pp. 405 ff.Google Scholar, and Tarski, Alfred, Grundzüge des Systemenkalküls, Fundamenta mathematicae, vol. 26 (1936), p. 293CrossRefGoogle Scholar.
3 A simpler procedure technically would be that of dispensing with f altogether, as is often done, and treating all variables as implicitly restricted to the field of g; but in most applications of sets of postulates some explicit restriction is required (e.g., fx = 0<x<1).
4 The argument extends to other types of dense series; it is first restricted for simplicity of presentation.
5 See Untersuchungen über die Axiome des Klassenkalkuls und über Produktations-und Summationsprobleme, welche gewisse Klassen von Aussagen betreffen, Skrifter utgit av Videnskapsselskapet i Kristiania, I. Matematisk-naturvidenskabelig klasse 1919, no. 3Google Scholar.
6 A problem of deducibility in the sense here intended must not on this account be confused with a decision problem (Entscheidungsproblem) in the usual sense; for, given a complete solution of the relevant decision problem, it would require an infinite number of applications of the decision procedure to answer affirmatively a question of deducibility.
7 Cf. Lewis and Langford, loc. cit.
- 1
- Cited by


