Article contents
Term models for weak set theories with a universal set
Published online by Cambridge University Press: 12 March 2014
Extract
We shall be concerned here with weak axiomatic systems of set theory with a universal set. The language in which they are expressed is that of set theory—two primitive predicates, = and ϵ, and no function symbols (though some function symbols will be introduced by definitional abbreviation). All the theories will have stratified axioms only, and they will all have Ext (extensionality: (∀x)(∀y)(x = y· ↔ ·(∀z)(z ϵ x ↔ z ϵ y))). In fact, in addition to extensionality, they have only axioms saying that the universe is closed under certain set-theoretic operations, viz. all of the form
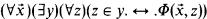
and these will always include singleton, i.e., ι′x exists if x does (the iota notation for singleton, due to Russell and Whitehead, is used here to avoid confusion with {x: Φ}, set abstraction), and also x ∪ y, x ∩ y and − x (the complement of x). The system with these axioms is called NF2 in the literature (see [F]). The other axioms we consider will be those giving ⋃x, ⋂x, {y: y ⊆x} and {y: x ⊆ y}. We will frequently have occasion to bear in mind that 〈 V, ⊆ 〉 is a Boolean algebra in any theory extending NF2. There is no use of the axiom of choice at any point in this paper. Since the systems with which we will be concerned exhibit this feature of having, in addition to extensionality, only axioms stating that V is closed under certain operations, we will be very interested in terms of the theories in question. A T-term, for T such a theory, is a thing (with no free variables) built up from V or ∧ by means of the T-operations, which are of course the operations that the axioms of T say the universe is closed under.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
- 3
- Cited by


