Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T12:47:06.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Taking out LK parts from a proof in Peano arithmetic1

Published online by Cambridge University Press:  12 March 2014

Tsuyoshi Yukami
Tsuyoshi Yukami*
Affiliation:
Institute of Mathematics, University of Tsukuba, Ibaraki 305, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let PA be Peano arithmetic with function symbols′, + and ·. The length of a proof P, denoted by lh(P), is the maximum length of threads of P (for the term ‘thread’, see [T, p. 14]). For a formula A and a natural number m, PA ⊢mA denotes the fact that there is a proof in PA of A whose length is less than or equal to m. PA ⊢ A denotes the fact that there is a proof in PA of A.

G. Kreisel conjectured that the following proposition holds.

“Let m be a natural number and A(a) be a formula. If for each natural number n, then PA ⊢ ∀xA(x)”.

Let PA1 be the corresponding system with + and · replaced by ternary predicates and axioms saying that these predicates represent functions. Parikh [P] proved the following proposition which is obtained from Kreisel's conjecture by replacing PA by PA1.

Proposition. Let A(a) be a formula in PA1and m be a natural number. Assume thatfor each natural number n. Then PA1 ⊢ ∀xA(x).

The reason why Parikh's method succeeds is the fact that the only function symbol ′ in PA1 is unary. So his method fails for PA.

To solve this conjecture for PA, we must make syntactical investigation into proofs in PA of formulas of the form A(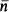) with length ≤ m. Even if lengths of proofs are less than or equal to m, depths of occurrences of bound variables in induction axiom schemata or equality axiom schemata in proofs are not always bounded.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 3 , September 1986 , pp. 682 - 700
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This research was partially supported by grant-in-aid for scientific research no. 59340011, Ministry of Education.

References

REFERENCES

[P]Parikh, R., Some results on the lengths of proofs, Transactions of the American Mathematical Society, vol. 177 (1973), pp. 29–36.CrossRefGoogle Scholar
[R]Richardson, D., Sets of theorems with short proofs, this Journal, vol. 39 (1974), pp. 235–242.Google Scholar
[S]Statman, R., Bounds for proof-search and speed-up in the predicate calculus, Annals of Mathematical Logic, vol. 15 (1978), pp. 225–287.CrossRefGoogle Scholar
[T]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1975.Google Scholar
[Y1]Yukami, T., A theorem on the formalized arithmetic with function symbols' and +, Tsukuba Journal of Mathematics, vol. 1 (1977), pp. 195–211.CrossRefGoogle Scholar
[Y2]Yukami, T., A theorem on lengths of proof of Presburger formulas, Tsukuba Journal of Mathematics, vol. 7 (1983), pp. 169–184.CrossRefGoogle Scholar