Syntactic translations and provably recursive functions

Extract

Syntactic translations of classical logic C into intuitionistic logic I are well known (see [Kol25], [Gli29], [Göd32], [Kre58b], [M063], [Cel69] and [Lei71]). Harvey Friedman [Fri78] used a translation of a similar nature, from I into itself, to reprove a theorem of Kreisel [Kre58a] that various theories based on I are closed under Markov's rule: if ¬¬∃x.α is a theorem, where x is a numeric variable and α is a primitive recursive relation, then ∃x.α is a theorem. Composing this with Gödel's translation from classical to intuitionistic theories, it follows that the functions provably recursive in the classical version of the theories considered are provably recursive already in their intuitionistic version. This conservation result is important in that it guarantees that no information about the convergence of recursive functions is lost when proofs are restricted to constructive logic, thus removing a potential objection to the use of constructive logic in reasoning about programs (see [C078] for example). Conversely, no objection can be raised by intuitionists to proofs of 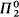formulas that use classical reasoning, because such proofs can be converted to constructive proofs (this has been exploited extensively; see [Smo82]).

Proofs of closure under Markov's rule had required, until Friedman's proof, a relatively sophisticated mathematical apparatus. The chief method used Godel's “Dialectica” interpretation (see [Tro73, §3]). Other proofs used cut-elimination, provable reflection for subsystems [Gir73], and Kripke models [Smo73]. Moreover, adapting these proofs to new theories had required that the underlying meta-mathematical techniques be adapted first, not always a trivial step.