Article contents
Sur la structuration du tableau des connectifs interpropositionnels binaires
Published online by Cambridge University Press: 12 March 2014
Extract
La théorie de la quaternalité, telle que Piaget et Gottschalk l'ont appliquée aux connectifs binaires du calcul bivalent, appelle quelques précisions et compléments.
Les seize connectifs ne comportent que deux quaternes complets: celui des jonctions et celui des implications. Leurs similitudes formelles ne doivent pas dissimuler une différence dans leur mode de construction. Elle apparaît sur leurs diagrammes (inspirés du “carré logique” traditionnel) par la place de la cellule initiale et par celles des signes barrés du trait vertical de la négation:
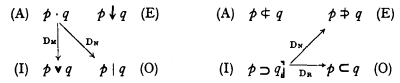
En effet, la dualité qui se combine avec celle de la négation contradictoire (DN, flèche diagonale) est, pour les jonctions, la dualité “morganienne” (DM, flèche verticale) et pour les implications, la dualité des réciproques (DR, flèche horizontale). Car dans les jonctions, liaisons symétriques, il n'y a point de vraies réciproques; inversement, les implications ne comportent pas (pourvu, bien sûr, qu'on ne les traduise pas en termes de jonctions) de dualité morganienne. Le quatrième terme, obtenu par la combinaison des deux relations génératrices, sera donc, pour les jonctions, une contreduale (DM × DN) et, pour les implications, une contreréciproque (DR × DN).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1957
References
1 Piaget, J., Traité de logique, §31 (1949)Google Scholar; Gottschalk, W. H., The theory of quaternality, ce Journal, vol. 18 (1953), pp. 193–196Google Scholar.
2 Nous avons étudié avec quelque détail cette structure abstraite de l'hexagone logique,” avec de nombreux exemples de ses applications diverses, dans un article Sur l'opposition des concepts, Theoria, vol. 19 (1953), pp. 89–130Google Scholar.
3 Pour ne pas surcharger le tableau, nous n'y avons inscrit que les flèches de la subalternation.
- 13
- Cited by


