Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T06:27:18.398Z Has data issue: false hasContentIssue false
  • English
  • Français

A structure theorem for semibounded sets in the reals

Published online by Cambridge University Press:  12 March 2014

Ya'acov Peterzil
Ya'acov Peterzil*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
*
Department of Mathematics, McGill University, Montreal, Quebec, CanadaH3A 2K6, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In [MPP] it was shown that in every reduct 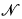of 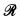= ‹ ℝ, +, ·, <› that properly expands ℳ = ‹ℝ, +, <, λa›a∈ℝ, all the bounded semi-algebraic (that is, 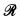-definable) sets are definable. Said differently, every such 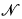is an expansion of 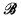= ‹ℝ, +, <, λa, Bi›a∈ℝ, i∈I where {Bi}i∈I is the collection of all bounded semialgebraic sets and the λa's are scalar multiplication by a. In [PSS] (see Theorem 1.2 below) it was shown that the structure 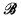is a proper reduct of 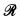; that is, one cannot define in it all the semialgebraic sets. In [Pe] we show that 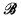is the only reduct properly between ℳ and 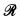. As a first step towards this result, we investigate in this paper the definable sets in reducts such as 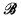. (We point out that ‘definable’ will always mean ‘definable with parameters’.)

Definition 1.1. Let X ⊆ ℝn. X is called semi-bounded if it is definable in the structure ‹ℝ, +, <, λa, B1, …, Bk›a∈ℝ, where the Bi's are bounded subsets of ℝn.

The main result of this paper (see Theorem 3.1) shows roughly that, in Ominimal expansions of 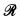that satisfy the partition condition (see Definition 2.3), every semibounded set can be partitioned into finitely many sets, each of which is of a form similar to a cylinder. Namely, these sets are obtained through the “stretching” of a bounded cell by finitely many linear vectors. As a corollary (see Theorem 1.4), we get different characterizations of semibounded sets, either in terms of their structure or in terms of their definability power.

The following result, by A. Pillay, P. Scowcroft and C. Steinhorn, was the main motivation for this paper. The theorem is formulated here in a slightly stronger form than originally, but the proof itself is essentially the original one. A short version of the proof is included in §4.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 779 - 794
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BCR]Bochnak, J., Coste, M. and Roy, M.-F., Géométrie algébrique réelle, Springer-Verlag, Berlin, 1988.Google Scholar
[KPS]Knight, J., Pillay, A. and Steinhorn, C., Definable sets in ordered structures. II, Transactions of the American Mathematical Society, vol. 295 (1986), pp. 593–605.CrossRefGoogle Scholar
[MPP]Marker, D., Peterzil, Y. and Pillay, A., Additive reducts of real closed fields, this Journal, vol. 57 (1992), pp. 109–117.Google Scholar
[Pe]Peterzil, Y., Some definability questions in structures over the reals and in general O-minimal structures, Ph.D. thesis, University of California, Berkeley, California, 1991.Google Scholar
[Pi]Pillay, A., On groups and fields definable in O-minimal structures, Journal of Pure and Applied Algebra, vol. 53 (1988), pp. 239–235.CrossRefGoogle Scholar
[PS]Pillay, A. and Steinhorn, C., Definable sets in ordered structures. I, Transactions of the American Mathematical Society, vol. 295 (1986), pp. 565–592.CrossRefGoogle Scholar
[PSS]Pillay, A., Scowcroft, P. and Steinhorn, C., Between groups and rings, Rocky Mountain Journal of Mathematics, vol. 9 (1989), pp. 871–885.Google Scholar
[vdD]van den Dries, L., On the elementary theory of restricted analytic functions, this Journal, vol. 53 (1988), pp. 796–808.Google Scholar