Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T07:28:14.788Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure of algebraically and existentially closed Stone and double Stone algebras

Published online by Cambridge University Press:  12 March 2014

David M. Clark
David M. Clark*
Affiliation:
Department of Mathematics and Computer Science, State University of New York, College at New Paltz New Paltz, New York 12561
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we study the varieties of Stone algebras (S, ∧, ∨, *, 0, 1) and double Stone algebras (D, ∧, ∨, *, +, 0, 1). Our primary interest is to give a structural description of the algebraically and existentially closed members of both classes. Our technique is an application of the natural dualities of Davey [6] and Clark and Krauss [5]. This approach gives a description of the desired models as the algebras of all continuous structure-preserving maps from certain structured Boolean spaces into the generating algebra for the variety. In each case the resulting description can be converted in a natural way into a finite ∀∃-axiomatization for these models. For Stone algebras these axioms appeared earlier in Schmid [20], [21] and in Schmitt [22].

Since both cases we consider satisfy the amalgamation property, the existentially closed members form a model companion for the variety which is also its model completion. Moreover, it is also ℵ0 categorical and its countably infinite member is the unique countable homogeneous universal model for the variety. In the case of Stone algebras, explicit constructions for this model appear in Schmitt [22] and Weispfenning [23]. We give here an explicit construction for double Stone algebras of S. Hayes.

This work was motivated by a problem of Stanley Burris. In [4] Burris and Werner superseded many previous results by showing that for any finite algebra A, the universal Horn class ISP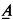 has a model companion. Weispfenning [24], [25] discovered that this model companion is always ℵ0 categorical and has a primitive recursive ∀∃-axiomatization. In spite of these very general theorems, there are few instances in which a structural description of the (any!) existentially closed members of ISP 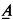is available. Burris and Werner [4] solve this problem in a special setting.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 363 - 375
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, K. A. and Pixley, A. F., Polynomial interpolation and the Chinese remainder theorem for algebraic systems, Mathematische Zeitschrift, vol. 143 (1973), pp. 165–174.CrossRefGoogle Scholar
[2]Balbes, R. and Dwinger, P., Distributive lattices, University of Missouri Press, Columbia, Missouri, 1974.Google Scholar
[3]Burris, S., Model companions for finitely generated universal Horn classes, this Journal, vol. 49 (1984), pp. 68–74.Google Scholar
[4]Burris, S. and Werner, H., Sheaf constructions and their elementary properties, Transactions of the American Mathematical Society, vol. 248 (1979), pp. 269–309.CrossRefGoogle Scholar
[5]Clark, D. M. and Krauss, P. H., Topological quasivarieties, Acta Universitatis Szegediensis. Acta Scientiarum Mathematicarum, vol. 47 (1984), pp. 3–39.Google Scholar
[6]Davey, B. A., Dualities for Stone algebras, double Stone algebras, and relative Stone algebras, Colloquium Mathematicum, vol. 46 (1982), pp. 1–14.CrossRefGoogle Scholar
[7]Davey, B. A. and Werner, H., Dualities and equivalences for varieties of algebras, Contributions to lattice theory (Szeged, 1980), Colloquia Mathematica Societatis János Bolyai, vol. 33, North-Holland, Amsterdam, 1983, pp. 101–275.Google Scholar
[8]Day, A., Varieties of Heyting algebras. II: Amalgamation and injectivity, preprint.Google Scholar
[9]Eklof, P. and Sabbagh, G., Model completions and modules, Annals of Mathematical Logic, vol. 2 (1970), pp. 251–295.CrossRefGoogle Scholar
[10]Grätzer, G. and Lakser, H., The structure of pseudocomplemented distributive lattices. II: Congruence extension and amalgamation, Transactions of the American Mathematical Society, vol. 156 (1971), pp. 343–358.Google Scholar
[11]Jónsson, B., Homogeneous universal relational systems, Mathematica Scandinavia, vol. 8 (1960), pp. 137–142.CrossRefGoogle Scholar
[12]Katriňák, T., The structure of distributive double p-algebras. Regularity and congruences, Algebra Universalis, vol. 3 (1973), pp. 238–246.CrossRefGoogle Scholar
[13]Katriňák, T., Injective double Stone algebras, Algebra Universalis, vol. 4 (1974), pp. 259–267.CrossRefGoogle Scholar
[14]Krauss, P. H., Homogeneous universal models of universal theories, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 23 (1977), pp. 415–426.CrossRefGoogle Scholar
[15]Lakser, H., The structure of pseudocomplemented distributive lattices. I: Subdirect decomposition, Transactions of the American Mathematical Society, vol. 156 (1971), pp. 334–342.Google Scholar
[16]Lee, K. B., Equational classes of distributive pseudocomplemented lattices, Canadian Journal of Mathematics, vol. 22 (1970), pp. 881–891.CrossRefGoogle Scholar
[17]Priestley, H. A., Ordered topological spaces and the representation of distributive lattices, Proceedings of the London Mathematical Society, ser. 3, vol. 24 (1972), pp. 507–530.CrossRefGoogle Scholar
[18]Riedel, H., Existentially closed algebras and the Boolean product construction, Ph.D. thesis, University of Waterloo, Waterloo, Ontario, 1984.Google Scholar
[19]Schmid, J., Algebraically and existentially closed distributive lattices, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 25 (1979), pp. 525–530.CrossRefGoogle Scholar
[20]Schmid, J., Model companions for distributive p-algebras, this Journal, vol. 47 (1982), pp. 680–688.Google Scholar
[21]Schmid, J., Algebraically closed distributive p-algebras, Algebra Universalis, vol. 15 (1982), pp. 126–141.CrossRefGoogle Scholar
[22]Schmitt, P., The model completion of Stone algebras, Annales Scientifiques de l'Université de Clermont, no. 60, Série Mathématique, no. 13 (1976), pp. 135–155.Google Scholar
[23]Weispfenning, V., Stone algebras without prime model extensions (abstract), this Journal, vol. 42 (1977), pp. 115.Google Scholar
[24]Weispfenning, V., A note on ℵ0-categorical model companions, Archiv für Mathematische Logik und Grundlagenforschung, vol. 19 (1978), pp. 23–29.CrossRefGoogle Scholar
[25]Weispfenning, V., Efficient decision algorithms for locally finite theories, Algebraic algorithms and error-correcting codes (proceedings of AAEEC-3, Grenoble, 1985), Lecture Notes in Computer Science, vol. 229, Springer-Verlag, Berlin, 1986, pp. 262–273.Google Scholar