Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T22:50:50.109Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONGLY MINIMAL STEINER SYSTEMS I: EXISTENCE

Part of: Model theory Finite geometry and special incidence structures

Published online by Cambridge University Press:  22 October 2020

JOHN BALDWIN  and
GIANLUCA PAOLINI
JOHN BALDWIN
Affiliation:
DEPARTMENT OF MATHEMATICS, STATISTICS, AND COMPUTER SCIENCE UNIVERSITY OF ILLINOIS AT CHICAGOCHICAGO, USAE-mail: [email protected]
GIANLUCA PAOLINI
Affiliation:
DEPARTMENT OF MATHEMATICS “GIUSEPPE PEANO” UNIVERSITY OF TORINO, VIA CARLO ALBERTO 10 10123, ITALYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear space is a system of points and lines such that any two distinct points determine a unique line; a Steiner k-system (for 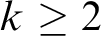$k \geq 2$ ) is a linear space such that each line has size exactly k. Clearly, as a two-sorted structure, no linear space can be strongly minimal. We formulate linear spaces in a (bi-interpretable) vocabulary 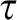$\tau $ with a single ternary relation R. 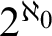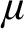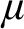We prove that for every integer k there exist $2^{\aleph _0}$ -many integer valued functions $\mu $ such that each $\mu $ determines a distinct strongly minimal Steiner k-system 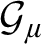$\mathcal {G}_\mu $ , whose algebraic closure geometry has all the properties of the ab initio Hrushovski construction. Thus each is a counterexample to the Zilber Trichotomy Conjecture.

Keywords

strongly minimalSteiner systemHrushovski construction

MSC classification

Primary: 03C45: Classification theory, stability and related concepts
Secondary: 51E10: Steiner systems
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1486 - 1507
Check for updates
Copyright
© Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baldwin, J. T., Fundamentals of Stability Theory, Springer-Verlag, New York, 1988.10.1007/978-3-662-07330-8CrossRefGoogle Scholar
Baldwin, J. T., Strongly minimal Steiner systems II: Coordinatizaton and strongly minimal quasigroups, in preparation, 2019.10.1017/jsl.2020.62CrossRefGoogle Scholar
Baldwin, J. T. and Shi, N., Stable generic structures . Annals of Pure and Applied Logic, vol. 79 (1996), pp. 1–35.10.1016/0168-0072(95)00027-5CrossRefGoogle Scholar
Barbina, S. and Casanovas, E., Model theory of Steiner triple systems, preprint, 2018, arXiv preprint arXiv:1805.06767.10.1142/S0219061320500105CrossRefGoogle Scholar
Cameron, P., Infinite linear spaces . Discrete Mathematics, vol. 129 (1994), pp. 29–41.10.1016/0012-365X(92)00503-JCrossRefGoogle Scholar
Cameron, P. J. and Webb, B. S., Perfect countably infinite Steiner triple systems . Australasian Journal of Combinatorics, vol. 54 (2012), pp. 273–278.Google Scholar
Conant, G. and Kruckman, A., Independence in generic incidence structures, preprint, 2016.Google Scholar
Evans, D., Block transitive Steiner systems with more than one point orbit . Journal of Combinatorial Design, vol. 12 (2004), pp. 459–464.10.1002/jcd.20018CrossRefGoogle Scholar
Evans, D. M. and Ferreira, M. S., The geometry of Hrushovski constructions, I: The uncollapsed case . Annals of Pure and Applied Logic, vol. 162 (2011), no. 6, pp. 474–488.10.1016/j.apal.2011.01.008CrossRefGoogle Scholar
Evans, D. M. and Ferreira, M. S., The geometry of Hrushovski constructions, II. The strongly minimal case, this Journal, vol. 77 (2012), no. 1, pp. 337–349.Google Scholar
Ganter, B. and Werner, H., Equational classes of Steiner systems . Algebra Universalis, vol. 5 (1975), pp. 125–140.10.1007/BF02485242CrossRefGoogle Scholar
Ganter, B. and Werner, H., Co-ordinatizing Steiner systems , Topics on Steiner Systems (Lindner, C. C. and Rosa, A., editors), North Holland, Amsterdam, 1980, pp. 3–24.10.1016/S0167-5060(08)70167-5CrossRefGoogle Scholar
Goode, J. B., Hrushovski’s geometries , Proceedings of 7th Easter Conference on Model Theory (Dahn, B. and Wolter, H., editors), Fachbereich Mathematik der Humboldt-Universität zu Berlin, Berlin, 1989, pp. 106–118.Google Scholar
Hasson, A. and Mermelstein, M., On the geometries of Hrushovski’s constructions. Fundamenta Mathematicae , 2018, to appear.Google Scholar
Holland, K., Model completeness of the new strongly minimal sets , this Journal, vol. 64 (1999), pp. 946–962.Google Scholar
Hrushovski, E., A new strongly minimal set . Annals of Pure and Applied Logic, vol. 62 (1993), pp. 147–166.10.1016/0168-0072(93)90171-9CrossRefGoogle Scholar
Hyttinen, T. and Paolini, G., First order model theory of free projective planes: Part I, submitted.Google Scholar
Lindström, P., On model completeness . Theoria, vol. 30 (1964), pp. 183–196.10.1111/j.1755-2567.1964.tb01088.xCrossRefGoogle Scholar
Makowsky, J. A., Can one design a geometry engine? On the (un)decidability of affine Euclidean geometries . Annals of Mathematics and Artificial Intelligence, vol. 85 (2019), pp. 259–291.10.1007/s10472-018-9610-1CrossRefGoogle Scholar
Mason, J. H., On a class of matroids arising from paths in graphs . Proceedings of the London Mathematical Society, vol. 25 (1972), pp. 55–74.10.1112/plms/s3-25.1.55CrossRefGoogle Scholar
Mermelstein, M., Infinite and Finitary Combinatorics Around Hrushovski Constructions, Ph.D. thesis, Ben-Gurion University of the Negev, 2018.Google Scholar
Paolini, G., New $\omega$ -stable planes, submitted.Google Scholar
Pillay, A., Model theory of algebraically closed fields , Model Theory and Algebraic Geometry: An Introduction to E. Hrushovski’s Proof of the Geometric Mordell-Lang Conjecture (Bouscaren, E., editor), Springer-Verlag, New York, 1999, pp. 61–834.Google Scholar
Stein, S. K., Foundations of quasigroups . Proceedings of the National Academy of Sciences of the United States of America, vol. 42 (1956), pp. 545–546.10.1073/pnas.42.8.545CrossRefGoogle ScholarPubMed
Stein, S. K., On the foundations of quasigroups . Transactions of the American Mathematical Society, vol. 85 (1957), pp. 228–256.10.1090/S0002-9947-1957-0094404-6CrossRefGoogle Scholar
Ziegler, M., An exposition of Hrushovski’s new strongly minimal set . Annals of Pure and Applied Logic, vol. 164 (2013), no. 12, pp. 1507–1519.10.1016/j.apal.2013.06.020CrossRefGoogle Scholar