No CrossRef data available.
Article contents
Strongly 2-dimensional theories
Published online by Cambridge University Press: 12 March 2014
Extract
In [8], we have shown the equivalence of almost strong minimality and strong unidimensionality. More precisely, we proved:
Theorem [8]. Let T be a countable stable theory. Then the following two conditions are equivalent:
(i) T is almost strongly minimal;
(ii) T can be extended to a theory such that any two nonalgebraic types are not almost orthogonal.
In the present paper, we define the notion of strong 2-dimensionality (of T). We show that if T is strongly 2-dimensional then T is ω-stable and its model has a simple structure. Roughly speaking, in a model of a strongly 2-dimensional theory, one of the following holds: (a) every element is in acl 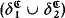 (δi is strongly minimal), or (b) every element is in acl
(δi is strongly minimal), or (b) every element is in acl 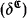 (δ is strongly regular). Shelah's definition of 2-dimensionality does not imply even superstability. (See Exercise 5.5 in [6, Chapter V, §5].) We show also that condition (a) above implies strong 2-dimensionality of T. However condition (b) does not imply strong 2-dimensionality in general.
(δ is strongly regular). Shelah's definition of 2-dimensionality does not imply even superstability. (See Exercise 5.5 in [6, Chapter V, §5].) We show also that condition (a) above implies strong 2-dimensionality of T. However condition (b) does not imply strong 2-dimensionality in general.
Our notations and conventions are standard. T is always countable and stable. We work in 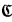 . A,B,… are used to denote small subsets of
. A,B,… are used to denote small subsets of 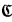 .
. 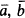 , … are used to denote finite sequences of elements in
, … are used to denote finite sequences of elements in 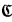 . δ, φ,… are used to denote formulas (with parameters), p, q, … are used to denote types (with parameters). The fact that p is a nonforking (forking) extension of q is denoted by p ⊃nfq(p ⊃fq). If p is stationary, p∣A denotes the type in S(A) which is parallel to p.
. δ, φ,… are used to denote formulas (with parameters), p, q, … are used to denote types (with parameters). The fact that p is a nonforking (forking) extension of q is denoted by p ⊃nfq(p ⊃fq). If p is stationary, p∣A denotes the type in S(A) which is parallel to p. 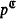 (or
(or 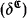 ) denotes the set of realizations of p (or δ). The Morley rank of p is denoted by RM(p).
) denotes the set of realizations of p (or δ). The Morley rank of p is denoted by RM(p).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1988


