Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T22:55:37.095Z Has data issue: false hasContentIssue false
  • English
  • Français

STRONG REDUCTIONS BETWEEN COMBINATORIAL PRINCIPLES

Published online by Cambridge University Press:  01 December 2016

DAMIR D. DZHAFAROV
DAMIR D. DZHAFAROV*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CONNECTICUT 196 AUDITORIUM ROAD STORRS, CT06269, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

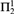This paper is a contribution to the growing investigation of strong reducibilities between ${\rm{\Pi }}_2^1$ statements of second-order arithmetic, viewed as an extension of the traditional analysis of reverse mathematics. We answer several questions of Hirschfeldt and Jockusch [13] about Weihrauch (uniform) and strong computable reductions between various combinatorial principles related to Ramsey’s theorem for pairs. Among other results, we establish that the principle 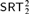$SRT_2^2$ is not Weihrauch or strongly computably reducible to 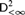$D_{ < \infty }^2$, and that COH is not Weihrauch reducible to 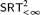$SRT_{ < \infty }^2$, or strongly computably reducible to 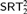$SRT_2^2$. The last result also extends a prior result of Dzhafarov [9]. We introduce a number of new techniques for controlling the combinatorial and computability-theoretic properties of the problems and solutions we construct in our arguments.

Keywords

Ramsey’s theoremreverse mathematicscomputability theoryWeihrauch reducibilitycomputable reducibility
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1405 - 1431
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brattka, V., Bibliography on Weihrauch Complexity , http://cca-net.de/publications/weibib.php.Google Scholar
Brattka, V., Gherardi, G., and Hölzl, R., Probabilistic computability and choice . Information and Computation, vol. 242 (2015), pp. 249–286.CrossRefGoogle Scholar
Brattka, V. and Rakotoniaina, T., On the Uniform Computational Content of Ramsey’s Theorem , submitted.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs , this JOURNAL, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
Chong, C. T., Lempp, S., and Yang, Y., On the role of the collection principle for ${\rm{\Sigma }}_2^0$ -formulas in second-order reverse mathematics . Proceedings of the American Mathematical Society, vol. 138 (2010), no. 3, pp. 1093–1100.Google Scholar
Chong, C. T., Slaman, T. A., and Yang, Y., The metamathematics of stable Ramsey’s theorem for pairs . Journal of the American Mathematical Society, vol. 27 (2014), no. 3, pp. 863–892.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.CrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic randomness and complexity, Theory and Applications of Computability, Springer, New York, 2010.CrossRefGoogle Scholar
Dzhafarov, D. D., Cohesive avoidance and strong reductions . Proceedings of the American Mathematical Society, vol. 143 (2015), no. 2, pp. 869–876.Google Scholar
Dzhafarov, D. D., The RM Zoo, 2015, http://rmzoo.uconn.edu.Google Scholar
Dzhafarov, D. D., Patey, L., Solomon, R., and Westrick, L. B.. Ramsey’s theorem for singletons and strong computable reducibility, to appear.Google Scholar
Hirschfeldt, D. R., Slicing the Truth: On the Computable and Reverse Mathematics of Combinatorial Principles, Lecture Notes Series/Institute for Mathematical Sciences, National University of Singapore, World Scientific Publishing Company Incorporated, New York, 2014.Google Scholar
Hirschfeldt, D. R. and Jockusch, C. G. Jr., On notions of computability theoretic reduction between ${\rm{\Pi }}_2^1$ principles, to appear.Google Scholar
Hirschfeldt, D. R., Jockusch, C. G. Jr., Kjos-Hanssen, B., Lempp, S., and Slaman, T. A., The strength of some combinatorial principles related to Ramsey’s theorem for pairs , Computational Prospects of Infinity. Part II. Presented Talks, Lecture Notes Series/Institute for Mathematical Sciences, National University of Singapore, vol. 15, World Scientific Publishing Company Incorporated, Hackensack, NJ, 2008, pp. 143–161.Google Scholar
[15] Hirschfeldt, D. R. and Shore, R. A., Combinatorial principles weaker than Ramsey’s theorem for pairs, this JOURNAL, vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
[16] Jockusch, C. G. Jr., Ramsey’s theorem and recursion theory, this JOURNAL, vol. 37 (1972), pp. 268–280.Google Scholar
Jockusch, C. G., Degrees of generic sets, Recursion Theory: Its Generalisation and Applications (Proc. Logic Colloq., Univ. Leeds, Leeds, 1979), London Mathematical Society Lecture Note Series, vol. 45, Cambridge University Press, Cambridge, 1980, pp. 110–139.Google Scholar
Mileti, J. R., Partition Theorems and Computability Theory , Ph.D thesis, University of Illinois at Urbana-Champaign, 2004.Google Scholar
Montalbán, A., Open questions in reverse mathematics . Bulletin of Symbolic Logic, vol. 17 (2011), no. 3, pp. 431–454.Google Scholar
Patey, L., The weakness of being cohesive, thin or free in reverse mathematics, submitted.Google Scholar
Rakotoniaina, T., The Computational Strength of Ramsey’s Theorem , Ph.D thesis, University of Cepe Town, 2015.Google Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem . Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582.Google Scholar
Shore, R. A., Lecture notes on turing degrees , Computational Prospects of Infinity II: AII Graduate Summer School, Lecture Notes Series/Institute for Mathematical Sciences, National University of Singapore, World Scientific Publishing Company Incorporated, Hackensack, NJ, to appear.Google Scholar
Simpson, S. G., Degrees of unsolvability: A survey of results , Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 631–652.Google Scholar
Simpson, S. G., Subsystems of second order arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.Google Scholar
Soare, R. I., Computability theory and applications , Theory and Applications of Computability, Springer, New York, to appear.Google Scholar
[27] Weihrauch, K., The Degrees of Discontinuity of Some Translators Between Representations of the Real Numbers , Informatik-Berichte 129, FernUniversität Hagen, 1992.Google Scholar