Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-16T23:32:24.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Strictly primitive recursive realizability, I

Published online by Cambridge University Press:  12 March 2014

Zlatan Damnjanovic
Zlatan Damnjanovic*
Affiliation:
School of Philosophy, University of Southern California, University Park, Los Angeles, California 90089
Get access Rights & Permissions [Opens in a new window]

Abstract

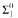A realizability notion that employs only primitive recursive functions is defined, and, relative to it, the soundness of the fragment of Heyting Arithmetic (HA) in which induction is restricted to formulae is proved. A dual concept of falsifiability is proposed and an analogous soundness result is established for a further restricted fragment of HA.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 4 , December 1994 , pp. 1210 - 1227
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Axt, P, Enumeration and the Grzegorczyk hierarchy, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 9 (1963), pp. 53–65.CrossRefGoogle Scholar
[2]Damnjanovic, Z., Elementary realizability (to appear).Google Scholar
[3]Grzegorczyk, A., Some classes of recursive functions, Rozprawy Matematyczne, vol. 4 (1953), pp. 1–46.Google Scholar
[4]Harrow, K., Equivalence of some hierarchies of primitive recursive functions, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 25 (1979), pp. 411–418.CrossRefGoogle Scholar
[5]Kleene, S. C., Introduction to metamathematics, Van Nostrand, New York, 1952.Google Scholar
[6]Kleene, S. C., Extension of an effectively generated class of functions by enumeration, Colloquium Mathematicum, vol. 6 (1958), pp. 67–78.CrossRefGoogle Scholar
[7]Leivant, D., Syntactic translations and provably recursive functions, this Journal, vol. 50 (1985), pp. 682–688.Google Scholar
[8]López-Escobar, E. G. K., Elementary interpretations of negationless arithmetic, Fundamenta Mathematicae, vol. 82 (1974), pp. 25–38.CrossRefGoogle Scholar
[9]Ritchie, R. W., Classes of recursive functions based on Ackermanns function, Pacific Journal of Mathematics, vol. 15 (1965), pp. 1027–1044.CrossRefGoogle Scholar
[10]Rose, H. E., Subrecursion: Functions and hierarchies, Clarendon Press, Oxford, 1984.Google Scholar
[11]Troelstra, A. S. (ed.), Metamathematical investigations of intuitionistic arithmetic and analysis, Springer-Verlag, New York, 1973.CrossRefGoogle Scholar
[12]Troelstra, A. S., Constructivism in mathematics: An introduction, vol. 1, North-Holland, Amsterdam, 1988.Google Scholar