Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T21:33:49.414Z Has data issue: false hasContentIssue false
  • English
  • Français

THE STRENGTH OF THE TREE THEOREM FOR PAIRS IN REVERSE MATHEMATICS

Published online by Cambridge University Press:  01 December 2016

LUDOVIC PATEY
LUDOVIC PATEY*
Affiliation:
LABORATOIRE PPS UNIVERSITÉ PARIS-DIDEROT - PARIS 7 CASE 7014, 75205 PARIS CEDEX 13 FRANCE E-mail: [email protected] URL: http://ludovicpatey.com
Get access Rights & Permissions [Opens in a new window]

Abstract

No natural principle is currently known to be strictly between the arithmetic comprehension axiom (ACA0) and Ramsey’s theorem for pairs ( 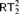$RT_2^2$ ) in reverse mathematics. The tree theorem for pairs ( 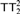$TT_2^2$ ) is however a good candidate. The tree theorem states that for every finite coloring over tuples of comparable nodes in the full binary tree, there is a monochromatic subtree isomorphic to the full tree. The principle 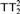$TT_2^2$ is known to lie between ACA0 and 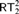$RT_2^2$ over RCA0, but its exact strength remains open. In this paper, we prove that 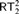$RT_2^2$ together with weak König’s lemma (WKL0) does not imply 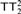$TT_2^2$ , thereby answering a question of Montálban. This separation is a case in point of the method of Lerman, Solomon and Towsner for designing a computability-theoretic property which discriminates between two statements in reverse mathematics. We therefore put the emphasis on the different steps leading to this separation in order to serve as a tutorial for separating principles in reverse mathematics.

Keywords

reverse mathematicsRamsey’s theoremtree theoremiterative forcing
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1481 - 1499
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bienvenu, L., Patey, L., and Shafer, P., On the logical strengths of partial solutions to mathematical problems, 2015, submitted, available at http://arxiv.org/abs/1411.5874.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs , this Journal, vol. 66 (2001), no. 01, pp. 1–55.Google Scholar
Chong, C., Slaman, T., and Yang, Y., The metamathematics of stable Ramsey’s theorem for pairs . Journal of the American Mathematical Society, vol. 27 (2014), no. 3, pp. 863–892.Google Scholar
Chubb, J., Hirst, J. L., and McNicholl, T. H., Reverse mathematics, computability, and partitions of trees , this Journal, vol. 74 (2009), no. 01, pp. 201–215.Google Scholar
Corduan, J., Groszek, M. J., and Mileti, J. R., Reverse mathematics and Ramsey’s property for trees , this Journal, vol. 75 (2010), no. 03, pp. 945–954.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.CrossRefGoogle Scholar
Dzhafarov, D. D., Cohesive avoidance and strong reductions . Proceedings of the American Mathematical Society, vol. 143 (2014), no. 2, pp. 869–876.CrossRefGoogle Scholar
Dzhafarov, D. D., Hirst, J. L., and Lakins, T. J., Ramsey’s theorem for trees: The polarized tree theorem and notions of stability . Archive for Mathematical Logic, vol. 49 (2010), no. 3, pp. 399–415.Google Scholar
Dzhafarov, D. D. and Jockusch, C. G., Ramsey’s theorem and cone avoidance , this Journal, vol. 74 (2009), no. 2, pp. 557–578.Google Scholar
Flood, S., Reverse mathematics and a Ramsey-type König’s lemma , this Journal, vol. 77 (2012), no. 4, pp. 1272–1280.Google Scholar
Flood, S. and Towsner, H., Separating principles below WKL 0, 2014, submitted. Available at http://arxiv.org/abs/1410.4068.Google Scholar
Friedman, H. M., Some systems of second order arithmetic and their use , Proceedings of the International Congress of Mathematicians, vol. 1, Canadian Mathematical Society, Montreal, Vancouver, 1974, pp. 235–242.Google Scholar
Frittaion, E. and Patey, L., Coloring the rationals in reverse mathematics, 2015, submitted, available at http://arxiv.org/abs/1508.00752.Google Scholar
Hirschfeldt, D. R., Slicing the Truth, Lecture Notes Series, Institute for Mathematical Sciences, vol. 28, National University of Singapore, World Scientific Publishing, Hackensack, NJ, 2014.Google Scholar
Hirschfeldt, D. R. and Jockusch, C. G., On notions of computability theoretic reduction between ${\rm{\Pi }}_2^1$ principles, to appear.Google Scholar
Jockusch, C. G., Ramsey’s theorem and recursion theory , this Journal, vol. 37 (1972), no. 2, pp. 268–280.Google Scholar
Lerman, M., Solomon, R., and Towsner, H., Separating principles below Ramsey’s theorem for pairs . Journal of Mathematical Logic, vol. 13 (2013), no. 02, p. 1350007.Google Scholar
Liu, L., RT 2 2 does not imply WKL 0 , this Journal, vol. 77 (2012), no. 2, pp. 609–620.Google Scholar
McNicholl, T. H., The inclusion problem for generalized frequency classes, Ph.D. thesis, George Washington University, ProQuest LLC, Ann Arbor, MI, 1995.Google Scholar
Mileti, J. R., Partition theorems and computability theory, Ph.D. thesis, Carnegie Mellon University, ProQuest LLC, Ann Arbor, MI, 2004.Google Scholar
Montalbán, A., Open questions in reverse mathematics , this Journal, vol. 17 (2011), no. 03, pp. 431–454.Google Scholar
Patey, L., A note on “Separating principles below Ramsey’s theorem for pairs”, (2013), unpublished. Available at http://ludovicpatey.com/media/research/note-em-sts.pdf.Google Scholar
Patey, L., Iterative forcing and hyperimmunity in reverse mathematics , Evolving Computability (Beckmann, Arnold, Mitrana, Victor, and Soskova, Mariya, editors), Lecture Notes in Computer Science, vol. 9136, Springer International Publishing, 2015, pp. 291–301.Google Scholar
Patey, L., Ramsey-type graph coloring and diagonal non-computability . Archive for Mathematical Logic, vol. 54 (2015), no. 7–8, pp. 899–914.Google Scholar
Patey, L., The weakness of being cohesive, thin or free in reverse mathematics, 2015, submitted. Available at http://arxiv.org/abs/1502.03709.Google Scholar
[26] Patey, L., The reverse mathematics of ramsey-type theorems , Ph.D. thesis, Université Paris Diderot, 2016.Google Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem , Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582.Google Scholar
Shoenfield, J. R., On degrees of unsolvability , Annals of Mathematics, vol. 69 (1959), no. 03, pp. 644–653.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Cambridge University Press, Cambridge, Association for Symbolic Logic, Poughkeepsie, NY, 2009.CrossRefGoogle Scholar