Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-30T23:42:27.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Stationary reflection and ideals

Published online by Cambridge University Press:  12 March 2014

Shu-Guo Zhang
Shu-Guo Zhang*
Affiliation:
Department of Mathematics, Institute of Mathematics, Sichuan University, Chengdu, Sichuan 610064, People'sRepublic of China
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we show that if there is a weakly normal ideal on κ then for each 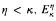fails. This greatly improves a theorem of C. A. Johnson.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 182 - 184
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jech, T., Stationary subsets of inaccessible cardinals, Axiomatic set theory, Contemporary Mathematics (Baumgartner, J.et al., editors), vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 115–142.Google Scholar
[2]Jech, T. and Shelah, S., Full reflection of stationary sets below ℵω, this Journal, vol. 55 (1990), pp. 822–830.Google Scholar
[3]Magidor, M., Reflecting stationary sets, this Journal, vol. 47 (1982), pp. 755–771.Google Scholar
[4]Johnson, C. A., On ideals and stationary reflection, this Journal, vol. 54 (1989), pp. 568–575.Google Scholar
[5]Kanamori, A., Weakly normal filters and irregular ultrafilters, Transactions of the American Mathematical Society, vol. 220 (1976), pp. 393–399.CrossRefGoogle Scholar
[6]Kanamori, A. and Magidor, M., The evolution of large cardinal axioms in set theory, Higher set theorem, Lecture Notes in Mathematics (Müller, G. H. and Scott, D., editors), vol. 699, Springer-Verlag, Berlin, 1978, pp. 99–275.Google Scholar
[7]Prikry, K., On descendingly complete ultrafilters, Cambridge summer school in mathematical logic, Lecture Notes in mathematics (Mathias, A. R. D. and Rogers, H., editors), vol. 337, Springer-Verlag, Berlin, 1973, pp. 459–488.Google Scholar
[8]Shelah, S., More on stationary coding, Around classification of models, Lecture Notes in Math., vol. 1182, Springer-Verlag, Berlin, 1986, pp. 224–246.Google Scholar
[9]Jensen, R., Donder, H. D. and Koppelberg, B., Some applications of the core model, Set theory and model theory, Lecture Notes in Mathematics (Jensen, R. and Prestel, A., editors), vol. 872, Springer-Verlag, Berlin, 1981, pp. 55–97.Google Scholar