Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ibarlucía, Tomás
2016.
The dynamical hierarchy for Roelcke precompact Polish groups.
Israel Journal of Mathematics,
Vol. 215,
Issue. 2,
p.
965.
Hamel, Clovis
and
Tall, Franklin D.
2020.
Model theory for Cp-theorists.
Topology and its Applications,
Vol. 281,
Issue. ,
p.
107197.
Khanaki, Karim
2022.
Dividing lines in unstable theories and subclasses of Baire 1 functions.
Archive for Mathematical Logic,
Vol. 61,
Issue. 7-8,
p.
977.


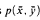 .
.