Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T11:32:55.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable embeddedness and NIP

Published online by Cambridge University Press:  12 March 2014

Anand Pillay
Anand Pillay*
Affiliation:
School of Mathematics, University of Leeds, Leeds, LS2 9JT, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give some sufficient conditions for a predicate P in a complete theory T to be “stably embedded”. Let 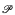be P with its “induced ∅-definable structure”. The conditions are that 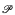(or rather its theory) is “rosy”. P has NIP in T and that P is stably 1-embedded in T. This generalizes a recent result of Hasson and Onshuus [6] which deals with the case where P is o-minimal in T. Our proofs make use of the theory of strict nonforking and weight in NIP theories ([3], [10]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 665 - 672
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adler, H., A geometric introduction to forking and thorn forking, 2007, preprint.Google Scholar
[2]Adler, H., Introduction to theories without the independence property, Archive for Mathematical Logic, to appear.Google Scholar
[3]Chernikov, A. and Kaplan, I., Forking and dividing in NTP2 theories, to appear in this Journal, number 147 on the MODNET preprint server.Google Scholar
[4]Ealy, C., Krupinski, K., and Pillay, A., Superrosy dependent groups having finitely satisfiable generics, Annals of Pure and Applied Logic, vol. 151 (2008), pp. 1–21.CrossRefGoogle Scholar
[5]Ealy, C. and Onshuus, A., Characterizing rosy theories, this Journal, vol. 72 (2007), pp. 919–940.Google Scholar
[6]Hasson, A. and Onshuus, A., Embedded o-minimal structures, Bulletin of the London Mathematical Society, vol. 42 (2010), pp. 64–74.CrossRefGoogle Scholar
[7]Hrushovski, E. and Pillay, A., On NIP and invariant measures, preprint 2009 (revised version), http://arxiv.org/abs/0710.2330.Google Scholar
[8]Onshuus, A., Properties and consequences of thorn independence, this Journal, vol. 71 (2006), pp. 1–21.Google Scholar
[9]Poizat, B., A course in model theory; an introduction to contemporary mathematical logic, Springer, 2000.Google Scholar
[10]Shelah, S., Dependent first order theories, continued, Israel Journal of Mathematics, vol. 173 (2009), pp. 1–60.CrossRefGoogle Scholar
[11]Usvyatsov, A., Morley sequences in dependent theories, preprint, http://arxiv.org/abs/0810.0733.Google Scholar