Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jäger, Gerhard
Kahle, Reinhard
and
Strahm, Thomas
1999.
Logic and Foundations of Mathematics.
p.
83.
Strahm, Thomas
2000.
The non-constructive μ operator, fixed point theories with ordinals, and the bar rule.
Annals of Pure and Applied Logic,
Vol. 104,
Issue. 1-3,
p.
305.
Strahm, Thomas
2003.
Theories with self-application and computational complexity.
Information and Computation,
Vol. 185,
Issue. 2,
p.
263.
Kahle, Reinhard
2003.
Universes over Frege structures.
Annals of Pure and Applied Logic,
Vol. 119,
Issue. 1-3,
p.
191.
Steiner, David
and
Strahm, Thomas
2006.
On the proof theory of type two functionals based on primitive recursive operations.
Mathematical Logic Quarterly,
Vol. 52,
Issue. 3,
p.
237.
Afshari, Bahareh
and
Rathjen, Michael
2010.
A note on the theory of positive induction, $${{\rm ID}^*_1}$$.
Archive for Mathematical Logic,
Vol. 49,
Issue. 2,
p.
275.
Leigh, Graham Emil
and
Rathjen, Michael
2010.
An ordinal analysis for theories of self-referential truth.
Archive for Mathematical Logic,
Vol. 49,
Issue. 2,
p.
213.
SATO, Kentaro
and
Zumbrunnen, Rico
2015.
A new model construction by making a detour via intuitionistic theories I: Operational set theory without choice is Π1-equivalent to KP.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 2,
p.
121.
Jäger, Gerhard
and
Strahm, Thomas
2017.
Reflections on the Foundations of Mathematics.
p.
270.


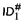 which results from
which results from 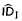 by restricting induction on the natural numbers to formulas which are positive in the fixed point constants, (ii) the theory BON(
by restricting induction on the natural numbers to formulas which are positive in the fixed point constants, (ii) the theory BON(