Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T16:43:03.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Some remarks on openly generated Boolean algebras

Published online by Cambridge University Press:  12 March 2014

Sakaé Fuchino
Sakaé Fuchino*
Affiliation:
Institut für Mathematik II, Freie Universität Berlin, W-1000 Berlin 33, Federal Republic of Germany E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Boolean algebra B is said to be openly generated if {A : A ≤rcB, ∣A∣ = ℵ0} includes a club subset of 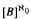. We show:

(V = L). For any cardinal κ there exists an L∞κ-free Boolean algebra which is not openly generated (Proposition 4.1).

(MA+(σ-closed)). Every 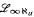-free Boolean algebra is openly generated (Theorem 4.2).

The last assertion follows from a characterization of openly generated Boolean algebras under MA+(σ-closed) (Theorem 3.1). Using this characterization we also prove the independence of problem 7 in Ščepin [15] (Proposition 4.3 and Theorem 4.4).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 302 - 310
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Bandlow, I., Factorization theorems and ‘strong’ sequences in bicompacta, Soviet Mathematics Doklady, vol. 22 (1980), pp. 196–200.Google Scholar
[2] Barwise, J. and Feferman, S. (Editors), Model-theoretic logics, Springer-Verlag, New York, Heidelberg, Berlin, 1985.Google Scholar
[3] Baumgartner, J. E., Applications of the proper forcing axiom, Handbook of set theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, New York, Oxford, 1984.Google Scholar
[4] Eklov, P. C., Applications to algebra, Model-theoretic logics (Barwise, J. and Feferman, S., editors), Springer-Verlag, New York, Heidelberg, Berlin, 1985, pp. 423–441.Google Scholar
[5] Feng, Q. and Jech, T., Local clubs, reflection, and preserving stationary sets, Proceedings of the London Mathematical Society, vol. 58 (1989), pp. 237–257.CrossRefGoogle Scholar
[6] Foreman, M., Magidor, M., and Shelah, S., Martin's maximum, saturated ideals, and nonregular ultrafilters. part I, Annals of Mathematics, vol. 127 (1988).Google Scholar
[7] Fuchino, S., Potential embedding and versions of Martin's axiom, Notre Dame Journal of Symbolic Logic, vol. 33 (1992), pp. 481–492.Google Scholar
[8] Fuchino, S., Some problems of Ščepin on openly generated Boolean algebras, Proceedings of the 10th Easter Conference, Humboldt Universität, Berlin, 1993 (to appear).Google Scholar
[9] Fuchino, S., Koppelberg, S., and Takahashi, M., On L ∞κ-free Boolean algebras, Annals of Pure and Applied Logic, vol. 55 (1992), pp. 265–284.CrossRefGoogle Scholar
[10] Heindorf, L., Openly generated Boolean algebras, mimeograph dated on 10 9, 1992.Google Scholar
[11] Jech, J., Multiple forcing, Cambridge University Press, London and New York, 1987.CrossRefGoogle Scholar
[12] Koppelberg, S., General theory of Boolean algebras, Handbook of Boolean Algebras, vol. 1 (Monk, J. D. and Bonnet, R., editors), North-Holland, Amsterdam, New York, Oxford, Tokyo, 1989.Google Scholar
[13] Koppelberg, S., Projective Boolean algebras, Handbook of Boolean Algebras, vol. 3 (Monk, J. D. with Bonnet, R., editors), North-Holland, Amsterdam, New York, Oxford, Tokyo, 1989, pp. 741–773.Google Scholar
[14] Kueker, D., -elementarily equivalent models of power ω1, Logic year 1979–80, Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin and New York, 1981, pp. 120–131.CrossRefGoogle Scholar
[15] Ščepin, E. V., Functors and uncountable powers of compacta, Uspechi Matematicheskikh Nauk, vol. 36 (1981), pp. 3–62; English translation, Russian Mathematical Suveys, vol. 36 (1981), pp. 1–71.Google Scholar
[16] Shelah, S., Semiproper forcing axiom implies Martin's maximum but not PFA+, this Journal, vol. 52 (1987), pp. 360–367.Google Scholar