Some remarks on definable equivalence relations in O-minimal structures

Extract

Let M be an O-minimal structure. We use our understanding, acquired in [KPS], of the structure of definable sets of n-tuples in M, to study definable (in M) equivalence relations on Mⁿ. In particular, we show that if E is an A-definable equivalence relation on Mⁿ (A ⊂ M) then E has only finitely many classes with nonempty interior in Mⁿ, each such class being moreover also A-definable. As a consequence, we are able to give some conditions under which an O-minimal theory T eliminates imaginaries (in the sense of Poizat [P]).

If L is a first order language and M an L-structure, then by a definable set in M, we mean something of the form X ⊂ Mⁿ, n ≥ 1, where X = {(a₁…,a_n) ∈ Mⁿ: M ⊨ϕ(ā)} for some formula 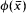∈ L(M). (Here L(M) means L together with names for the elements of M.) If the parameters from 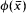come from a subset A of M, we say that X is A-definable.

M is said to be O-minimal if M = (M, <,…), where < is a dense linear order with no first or last element, and every definable set X ⊂ M is a finite union of points, and intervals (a, b) (where a, b ∈ M ∪ {± ∞}). (This notion is as in [PS] except here we demand the underlying order be dense.) The complete theory T is said to be O-minimal if every model of T is O-minimal. (Note that in [KPS] it is proved that if M is O-minimal, then T = Th(M) is O-minimal.) In the remainder of this section and in §2, M will denote a fixed but arbitrary O-minimal structure. A,B,C,… will denote subsets of M.