Article contents
Some highly saturated models of Peano arithmetic
Published online by Cambridge University Press: 12 March 2014
Extract
Some highly saturated models of Peano Arithmetic are constructed in this paper, which consists of two independent sections. In § 1 we answer a question raised in [10] by constructing some highly saturated, rather classless models of PA. A question raised in [7], [3], ]4] is answered in §2, where highly saturated, nonstandard universes having no bad cuts are constructed.
Highly saturated, rather classless models of Peano Arithmetic were constructed in [10]. The main result proved there is the following theorem. If λ is a regular cardinal and 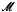 is a λ-saturated model of PA such that ∣M∣ > λ, then
is a λ-saturated model of PA such that ∣M∣ > λ, then 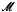 has an elementary extension
has an elementary extension 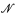 of the same cardinality which is also λ-saturated and which, in addition, is rather classless. The construction in [10] produced a model
of the same cardinality which is also λ-saturated and which, in addition, is rather classless. The construction in [10] produced a model 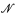 for which cf(
for which cf(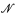 ) = λ+. We asked in Question 5.1 of [10] what other cofinalities could such a model
) = λ+. We asked in Question 5.1 of [10] what other cofinalities could such a model 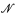 have. This question is answered here in Theorem 1.1 of §1 by showing that any cofinality not immediately excluded is possible. Its proof does not depend on the theorem from [10]; in fact, the proof presented here gives a proof of that theorem which is much simpler and shorter than the one in [10].
have. This question is answered here in Theorem 1.1 of §1 by showing that any cofinality not immediately excluded is possible. Its proof does not depend on the theorem from [10]; in fact, the proof presented here gives a proof of that theorem which is much simpler and shorter than the one in [10].
Recursively saturated, rather classless κ-like models of PA were constructed in [9]. In the case of singular κ such models were constructed whenever cf(κ) > ℵ0; no additional set-theoretic hypothesis was needed.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2002
References
REFERENCES
- 2
- Cited by


