Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T02:05:36.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Slow growing versus fast growing

Published online by Cambridge University Press:  12 March 2014

S. S. Wainer
S. S. Wainer*
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, England
Get access Rights & Permissions [Opens in a new window]

Extract

I falsely claimed, as an aside remark in [8] and also implicitly in the abstract [9], that the slow-growing hierarchy

“catches up” with the fast-growing hierarchy

at level Γ0, i.e. that, for all x > 0,

where x′ is some simple (even linear) function of x.

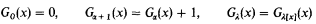
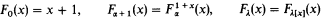
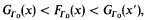
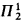Girard [4] gave the first correct analysis of the deep relationship which exists between G and F, based on his extensive category-theoretic framework for -logic. This analysis indicates that the first point at which G catches up with F is the ordinal of the theory ID<ω(0 of arbitrary finite iterations of an inductive definition. This is very far beyond Γ0! In particular, in order to capture F at level ∣IDn∣ the slow-growing hierarchy must be generated up to ∣IDn+1∣, i.e. one extra iteration of an inductive definition is needed in order to generate sufficient new ordinals.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 2 , June 1989 , pp. 608 - 614
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aczel, P., Another elementary treatment of Girard's result connecting the slow and fast growing hierarchies of number-theoretic functions, manuscript, 1980.Google Scholar
[2]Buchholz, W., Three contributions to the conference on recent advances in proof theory, manuscript, 1980.Google Scholar
[3]Cichon, E. A. and Wainer, S. S., The slow-growing and the Grzegorczyk hierarchies, this Journal, vol. 48 (1983), pp. 399–408.Google Scholar
[4]Girard, J.-Y., logic, Annals of Mathematical Logic, vol. 21 (1981), pp. 75–219.CrossRefGoogle Scholar
[5]Jervell, H. R., Homogeneous trees, Lecture notes, University of Munich, Munich, 1979.Google Scholar
[6]Schmerl, U. R., Über die schwach und die stark wachsende Hierarchie zahlentheoretischer Funktionen, Bayerische Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse. Sitzungsberichte, 1981, pp. 1–18.Google Scholar
[7]Schwichtenberg, H., Homogeneous trees and subrecursive hierarchies, Lecture, 1980.Google Scholar
[8]Wainer, S. S., Ordinal recursion and a refinement of the extended Grzegorczyk hierarchy, this Journal, vol. 37 (1972), pp. 287–292.Google Scholar
[9]Wainer, S. S., A subrecursive hierarchy over the predicative ordinals, Conference in mathematical logic—London 70 (Hodges, W., editor), Lecture Notes in Mathematics, vol. 255, Springer-Verlag, Berlin, 1972, pp. 350–351 (abstract #14).Google Scholar
[10]Wainer, S. S., The “slow-growing” approach to hierarchies, Recursion theory (Nerode, A. and Shore, R., editors), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, Rhode Island, 1985, pp. 487–502.CrossRefGoogle Scholar