Article contents
Skolem functions and elementary embeddings
Published online by Cambridge University Press: 12 March 2014
Extract
Let L be an elementary first order language. Let 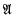 be an L-structure, and let φ be an L-formula with free variables u1, …, un, and υ. A Skolem function for φ on
be an L-structure, and let φ be an L-formula with free variables u1, …, un, and υ. A Skolem function for φ on 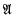 is an n-ary operation f on
is an n-ary operation f on 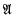 such that for all
such that for all 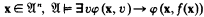 . If
. If 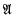 is an elementary substructure of
is an elementary substructure of 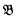 , then an n-ary operation f on
, then an n-ary operation f on 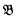 is said to preserve the elementary embedding of
is said to preserve the elementary embedding of 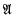 into
into 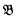 if f(x)∈
if f(x)∈ 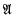 for all x ∈
for all x ∈ 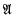 n, and (
n, and (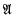 , f ∣
, f ∣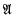 n) ≺ (
n) ≺ (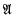 , f). Keisler asked the following question:
, f). Keisler asked the following question:
Problem 1. If 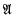 and
and 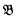 are L-structures such that
are L-structures such that 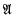 ≺
≺ 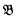 , and if φ (u, υ) is an L-formula (with appropriate free variables), must there be a Skolem function for φ on
, and if φ (u, υ) is an L-formula (with appropriate free variables), must there be a Skolem function for φ on 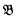 which preserves the elementary embedding?
which preserves the elementary embedding?
Payne [6] gave a counterexample in which the language L is uncountable. In [3], [5], the author announced the existence of an example in which L is countable but the structures 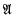 and
and 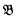 are uncountable. The construction of the example will be given in this paper. Keisler's problem is still open in case both the language and the structures are required to be countable. Positive results for some special cases are given in [4].
are uncountable. The construction of the example will be given in this paper. Keisler's problem is still open in case both the language and the structures are required to be countable. Positive results for some special cases are given in [4].
The following variant of Keisler's question was brought to the author's attention by Peter Winkler:
Problem 2. If L is a countable language, 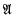 a countable L-structure, and φ(u, υ) an L-formula, must there be a Skolem function f for φ on
a countable L-structure, and φ(u, υ) an L-formula, must there be a Skolem function f for φ on 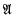 such that for every countable elementary extension
such that for every countable elementary extension 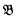 of
of 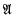 , there is an extension of f which preserves the elementary embedding of
, there is an extension of f which preserves the elementary embedding of 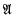 into
into 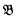 ?
?
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
References
REFERENCES
- 1
- Cited by


