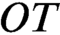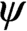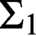Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Arai, Toshiyasu
2023.
Wellfoundedness proof with the maximal distinguished set.
Archive for Mathematical Logic,
Vol. 62,
Issue. 3-4,
p.
333.