The set theoretical foundations of nonstandard analysis

Extract

Nonstandard analysis was developed in [1] within a logic which has a language with finite types. In [2] and [3] the logic is first order and the language is that of set theory. The set theoretical approach can be described in the following setting.

Let 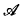be a relational structure (A, ∈) where A is a nonempty set and ∈ is a restriction of the elementhood relation of set theory.

Let Ext be the wf (∀x)[(∃w)[w ∈ x] → [(∀y)(∀z) [z ∈ x ↔ z ∈ y] → x = y]]. Call 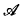a fragment of set theory if 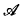⊧ Ext. By forming a nontrivial ultrapower of 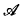one obtains a structure 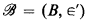which, after canonically embedding 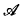in 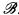, becomes a proper elementary extension of .

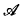Let j embed 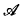canonically in 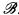. Let 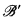be the substructure (B′, ∈′) of 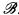where B′ is the ∈′-closure of j(A) in B. That is, B′ is the smallest subset of B containing j(A) such that if b ∈ B, b′ ∈ B′ and 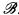⊧ b ∈ b′ then b ∈ B′.