Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T05:54:24.947Z Has data issue: false hasContentIssue false
  • English
  • Français

A second paper “On the interpolation theorem for the logic of constant domains”

Published online by Cambridge University Press:  12 March 2014

E.G.K. López-Escobar
E.G.K. López-Escobar*
Affiliation:
University of Maryland, College Park, Maryland 20742
Get access Rights & Permissions [Opens in a new window]

Extract

It was brought to our attention by M. Fitting that Beth's semantic tableau system using the intuitionistic propositional rules and the classical quantifier rules produces a correct but incomplete axiomatization of the logic CD of constant domains. The formula

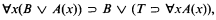
where T is a truth constant, being an instance of a formula which is valid in all Kripke models with constant domains but which is not provable without cut.

From the Fitting formula one can immediately obtain that the sequent

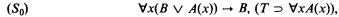
although provable in the system GD outlined in [3], does not have a cut-free proof (in the system GD).

If the only problem with GD were the sequent S0, then we could extend GD to the system GD+ by adding the following (correct) rule:

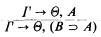
Since the new rule still satisfies the subformula property a cut elimination theorem for GD+ would be a step in the right direction for a syntactical proof for the interpolation theorem for the logic of constant domains (cf. Gabbay [2]; see also §4). Unfortunately, one can show that the sequent

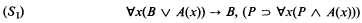
where P is a propositional parameter (or formula without x free) has a derivation in GD+, but does not have a cut-free derivation (in GD+). Of course, we could extend GD+ to GD++ by adding the following correct (and with the subformula property) rule:

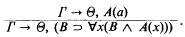
But then we can find a sequent S2 which, although provable with cut in GD++, does not have a cut-free derivation in GD++.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 3 , September 1983 , pp. 595 - 599
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Dummett, M., Elements of intuitionism, Oxford University Press, Oxford, 1977, p. 467.Google Scholar
[2]Gabbay, D., Craig interpolation theorem for intuitionistic logic and extensions. III, this Journal, vol. 42 (1977), pp. 269–271.Google Scholar
[3]Lopez-Escobar, E.G.K., On the interpolation theorem for the logic of constant domains, this Journal, vol. 46 (1981), pp. 87–88.Google Scholar