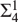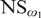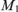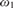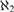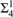Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2022.
A Model in Which Well-Orderings of the Reals Appear at a Given Projective Level.
Axioms,
Vol. 11,
Issue. 8,
p.
354.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2023.
A Model in Which Well-Orderings of the Reals First Appear at a Given Projective Level, Part II.
Mathematics,
Vol. 11,
Issue. 11,
p.
2517.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2024.
A good lightface Δn1 well-ordering of the reals does not imply the existence of boldface Δn−11 well-orderings.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 6,
p.
103426.