No CrossRef data available.
Article contents
THE REVERSE MATHEMATICS OF THE THIN SET AND ERDŐS–MOSER THEOREMS
Published online by Cambridge University Press: 24 November 2021
Abstract
The thin set theorem for n-tuples and k colors ( $\operatorname {\mathrm {\sf {TS}}}^n_k$
) states that every k-coloring of
$\operatorname {\mathrm {\sf {TS}}}^n_k$
) states that every k-coloring of  $[\mathbb {N}]^n$
admits an infinite set of integers H such that
$[\mathbb {N}]^n$
admits an infinite set of integers H such that 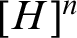 $[H]^n$
avoids at least one color. In this paper, we study the combinatorial weakness of the thin set theorem in reverse mathematics by proving neither
$[H]^n$
avoids at least one color. In this paper, we study the combinatorial weakness of the thin set theorem in reverse mathematics by proving neither  $\operatorname {\mathrm {\sf {TS}}}^n_k$
, nor the free set theorem (
$\operatorname {\mathrm {\sf {TS}}}^n_k$
, nor the free set theorem ( $\operatorname {\mathrm {\sf {FS}}}^n$
) imply the Erdős–Moser theorem (
$\operatorname {\mathrm {\sf {FS}}}^n$
) imply the Erdős–Moser theorem ( $\operatorname {\mathrm {\sf {EM}}}$
) whenever k is sufficiently large (answering a question of Patey and giving a partial result towards a question of Cholak Giusto, Hirst and Jockusch). Given a problem
$\operatorname {\mathrm {\sf {EM}}}$
) whenever k is sufficiently large (answering a question of Patey and giving a partial result towards a question of Cholak Giusto, Hirst and Jockusch). Given a problem 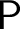 $\mathsf {P}$
, a computable instance of
$\mathsf {P}$
, a computable instance of 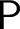 $\mathsf {P}$
is universal iff its solution computes a solution of any other computable
$\mathsf {P}$
is universal iff its solution computes a solution of any other computable 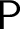 $\mathsf {P}$
-instance. It has been established that most of Ramsey-type problems do not have a universal instance, but the case of Erdős–Moser theorem remained open so far. We prove that Erdős–Moser theorem does not admit a universal instance (answering a question of Patey).
$\mathsf {P}$
-instance. It has been established that most of Ramsey-type problems do not have a universal instance, but the case of Erdős–Moser theorem remained open so far. We prove that Erdős–Moser theorem does not admit a universal instance (answering a question of Patey).
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



