Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T23:43:05.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Reverse mathematics and the equivalence of definitions for well and better quasi-orders

Published online by Cambridge University Press:  12 March 2014

Peter Cholak ,
Alberto Marcone  and
Reed Solomon
Peter Cholak
Affiliation:
Department of Mathematics, University of Notre Dame, 255 Hurley, Notre Dame, Indiana 46556-4618, USA, E-mail: [email protected]
Alberto Marcone
Affiliation:
Dipartimento di Matematica e Informatica, Università di Udine, Via Delle Scienze 206, 33100 Udine, Italy, E-mail: [email protected]
Reed Solomon
Affiliation:
Department of Mathematics, University of Connecticut, 196 Auditorium Road, Storrs, Connecticut 06269-3009, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In reverse mathematics, one formalizes theorems of ordinary mathematics in second order arithmetic and attempts to discover which set theoretic axioms are required to prove these theorems. Often, this project involves making choices between classically equivalent definitions for the relevant mathematical concepts. In this paper, we consider a number of equivalent definitions for the notions of well quasi-order and better quasi-order and examine how difficult it is to prove the equivalences of these definitions.

As usual in reverse mathematics, we work in the context of subsystems of second order arithmetic and take RCA0 as our base system. RCA0 is the subsystem formed by restricting the comprehension scheme in second order arithmetic to 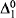formulas and adding a formula induction scheme for 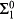formulas. For the purposes of this paper, we will be concerned with fairly weak extensions of RCA0 (indeed strictly weaker than the subsystem ACA0 which is formed by extending the comprehension scheme in RCA0 to cover all arithmetic formulas) obtained by adjoining certain combinatorial principles to RCA0. Among these, the most widely used in reverse mathematics is Weak König's Lemma; the resulting theory WKL0 is extensively documented in [11] and elsewhere.

We give three other combinatorial principles which we use in this paper. In these principles, we use k to denote not only a natural number but also the finite set {0, …, k − 1}.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 3 , September 2004 , pp. 683 - 712
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cholak, Peter, Jockusch, Carl, and Slaman, Ted, The strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[2]Downey, Rodney G., Computability theory and linear orderings, Handbook of recursive mathematics (Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), vol. 2, North-Holland, Amsterdam, 1998, pp. 823–976.Google Scholar
[3]Downey, Rodney G., Hirschfeldt, Denis R., Lempp, Steffen, and Solomon, Reed, Computability-theoretic and proof-theoretic aspects of partial and linear orderings, to appear in Israel Journal of Mathematics.Google Scholar
[4]Herrmann, Eberhard, Infinite chains and antichains in computable partial orderings, this Journal, vol. 66 (2001), no. 2, pp. 923–934.Google Scholar
[5]Hirschfeldt, Denis R. and Shore, Richard A., Some facts about linear orderings provable in , to appear.Google Scholar
[6]Marcone, Alberto, Wqo and bqo theory in subsystems of second order arithmetic, to appear in Simpson, S. G., editor. Reverse mathematics 2001.Google Scholar
[7]Marcone, Alberto, Foundations of bqo theory, Transactions of the American Mathematical Society, vol. 345 (1994), no. 2, pp. 641–660.CrossRefGoogle Scholar
[8]Milner, Eric C., Basic wqo- and bqo-theory, Graphs and order (Rival, Ivan, editor), D. Reidel, Dordrecht, 1985, pp. 487–502.CrossRefGoogle Scholar
[9]Simpson, Stephen G., Bqo theory and Fraïssé's conjecture, Recursive aspects of descriptive set theory (Mansfield, R. and Weitkamp, G., editors), Oxford University Press, Oxford, 1985, pp. 124–138.Google Scholar
[10]Simpson, Stephen G., Ordinal numbers and the Hilbert basis theorem, this Journal, vol. 53 (1988), no. 3, pp. 961–974.Google Scholar
[11]Simpson, Stephen G., Subsystems of second order arithmetic, Springer-Verlag, 1998.Google Scholar