Article contents
A result concerning cardinalities of ultraproducts1
Published online by Cambridge University Press: 12 March 2014
Extract
The cardinality problem for ultraproducts is as follows: Given an ultrafilter 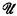 over a set I and cardinals αi, i ∈ I, what is the cardinality of the ultraproduct
over a set I and cardinals αi, i ∈ I, what is the cardinality of the ultraproduct 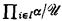 ? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter
? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter 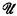 over a set I of power κ (uniform means that all elements of
over a set I of power κ (uniform means that all elements of 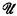 have power κ). It is open whether every countably incomplete
have power κ). It is open whether every countably incomplete 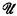 has the property that, for all infinite α, the ultra-power
has the property that, for all infinite α, the ultra-power 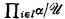 has power ακ. However, it is shown in [4] that certain countably incomplete
has power ακ. However, it is shown in [4] that certain countably incomplete 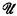 , namely the κ-regular
, namely the κ-regular 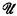 , have this property.
, have this property.
This paper is about another cardinality property of ultrafilters which was introduced by Eklof [1] to study ultraproducts of abelian groups. It is open whether every countably incomplete ultrafilter has the Eklof property. We shall show that certain countably incomplete ultrafilters, the κ-good ultrafilters, do have this property. The κ-good ultrafilters are important in model theory because they are exactly the ultrafilters 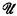 such that every ultraproduct modulo
such that every ultraproduct modulo 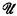 is κ-saturated (see [5]).
is κ-saturated (see [5]).
Let 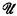 be an ultrafilter on a set I. Let αi, n, i ∈ I, n ∈ ω, be cardinals and αi, n, ≥ αi, m if n < m. Let
be an ultrafilter on a set I. Let αi, n, i ∈ I, n ∈ ω, be cardinals and αi, n, ≥ αi, m if n < m. Let
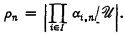 .
.
Then ρn are nonincreasing and therefore there is some m and ρ such that ρn = ρ if n ≥ m. We call ρ the eventual value (abbreviated ev val) of ρn.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
Footnotes
The preparation of this paper was supported by NSF grants GP-27633 and GP-27964.
References
REFERENCES
- 3
- Cited by


