Article contents
RESTRICTED MAD FAMILIES
Published online by Cambridge University Press: 05 November 2019
Abstract
Let 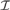 ${\cal I}$ be an ideal on ω. By cov
${\cal I}$ be an ideal on ω. By cov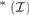 ${}_{}^{\rm{*}}({\cal I})$ we denote the least size of a family
${}_{}^{\rm{*}}({\cal I})$ we denote the least size of a family 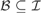 ${\cal B} \subseteq {\cal I}$ such that for every infinite
${\cal B} \subseteq {\cal I}$ such that for every infinite 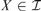 $X \in {\cal I}$ there is
$X \in {\cal I}$ there is 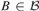 $B \in {\cal B}$ for which
$B \in {\cal B}$ for which 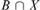 $B\mathop \cap \nolimits X$ is infinite. We say that an AD family
$B\mathop \cap \nolimits X$ is infinite. We say that an AD family 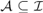 ${\cal A} \subseteq {\cal I}$ is a MAD family restricted to
${\cal A} \subseteq {\cal I}$ is a MAD family restricted to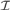 ${\cal I}$ if for every infinite
${\cal I}$ if for every infinite 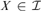 $X \in {\cal I}$ there is
$X \in {\cal I}$ there is 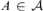 $A \in {\cal A}$ such that
$A \in {\cal A}$ such that 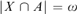 $|X\mathop \cap \nolimits A| = \omega$. Let a
$|X\mathop \cap \nolimits A| = \omega$. Let a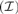 $\left( {\cal I} \right)$ be the least size of an infinite MAD family restricted to
$\left( {\cal I} \right)$ be the least size of an infinite MAD family restricted to 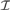 ${\cal I}$. We prove that If
${\cal I}$. We prove that If 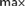 $max${a,cov
$max${a,cov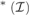 ${}_{}^{\rm{*}}({\cal I})\}$ then a
${}_{}^{\rm{*}}({\cal I})\}$ then a $\left( {\cal I} \right) = {\omega _1}$, and consequently, if
$\left( {\cal I} \right) = {\omega _1}$, and consequently, if 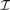 ${\cal I}$ is tall and
${\cal I}$ is tall and 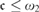 $\le {\omega _2}$ then a
$\le {\omega _2}$ then a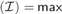 $\left( {\cal I} \right) = max$ {a,cov
$\left( {\cal I} \right) = max$ {a,cov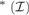 ${}_{}^{\rm{*}}({\cal I})\}$. We use these results to prove that if c
${}_{}^{\rm{*}}({\cal I})\}$. We use these results to prove that if c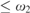 $\le {\omega _2}$ then o
$\le {\omega _2}$ then o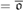 $= \overline o$ and that as
$= \overline o$ and that as $= max${a,non
$= max${a,non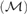 $({\cal M})\}$. We also analyze the problem whether it is consistent with the negation of CH that every AD family of size ω1 can be extended to a MAD family of size ω1.
$({\cal M})\}$. We also analyze the problem whether it is consistent with the negation of CH that every AD family of size ω1 can be extended to a MAD family of size ω1.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 7
- Cited by


