Article contents
Regular embeddings of the stationary tower and Woodin's 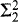 maximality theorem
maximality theorem
Published online by Cambridge University Press: 12 March 2014
Abstract
We present Woodin's proof that if there exists a measurable Woodin cardinal δ then there is a forcing extension satisfying all 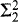 sentences ϕ such that CH + ϕ holds in a forcing extension of V by a partial order in Vδ. We also use some of the techniques from this proof to show that if there exists a stationary limit of stationary limits of Woodin cardinals, then in a homogeneous forcing extension there is an elementary embedding j: V → M with critical point
sentences ϕ such that CH + ϕ holds in a forcing extension of V by a partial order in Vδ. We also use some of the techniques from this proof to show that if there exists a stationary limit of stationary limits of Woodin cardinals, then in a homogeneous forcing extension there is an elementary embedding j: V → M with critical point 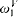 such that M is countably closed in the forcing extension.
such that M is countably closed in the forcing extension.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 1
- Cited by


