Recursive categoricity and persistence

Extract

This paper is concerned with recursive structures and the persistance of an effective notion of categoricity. The terminology and notational conventions are standard. We will devote the rest of this paragraph to a cursory review of some of the assumed conventions. If θ is a formula, then θ^k denotes θ if k is zero, and ¬θ if k is one. If A is a sequence with domain a subset of ω, then A∣ _n denotes the sequence obtained by restricting the domain of A to n. For an effective first order language L, let {c_i ∣i<ω} be distinct new constants, and let {θ _i ∣i<ω} be an effective enumeration of all sentences in the language L ∪ {c_i ∣j<ω}. An infinite L-structure 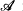is recursive iff it has universe ω and the set 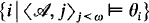is recursive, where c_n is interpreted by n. In general we say that a set of formulas is recursive if the set of its indices with respect to an enumeration such as above is recursive. The ∃-diagram of a structure 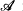is recursive if the structure is recursive and the set 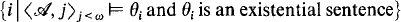and θ _i is an existential sentence} is also recursive. The definition of “the ∀∃-diagram of 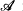is recursive” is similar.