No CrossRef data available.
Article contents
The reals in core models
Published online by Cambridge University Press: 12 March 2014
Abstract
We set 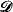 = ‹
= ‹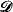 , ≤L , # ›, where
, ≤L , # ›, where 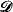 is the set of degrees of nonconstructibility for countable sets of countable ordinals. We show how to define inductively over this structure the degrees of such sets of ordinals in Κ, the core model, and the next few core models thereafter, i.e. without reference to mice, premice or measurable cardinals
is the set of degrees of nonconstructibility for countable sets of countable ordinals. We show how to define inductively over this structure the degrees of such sets of ordinals in Κ, the core model, and the next few core models thereafter, i.e. without reference to mice, premice or measurable cardinals
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
[CM]
Dodd, A. J., The core model, London Mathematical Society Lecture Note Series, no. 61, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[CU]
Beller, A., Jensen, R. and Welch, P., Coding the universe, London Mathematical Society Lecture Note Series, no. 47, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[K]
Kechris, A. S., The theory of countable analytical sets, Transactions of the American Mathematical Society, vol. 202 (1975), pp. 259–297.CrossRefGoogle Scholar
[W]
Welch, Philip, The natural hierarchy and quasi-hierarchy of L-degrees, this Journal, vol. 51 (1986), pp. 130–134.Google Scholar


