Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T15:51:41.047Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOMNESS NOTIONS AND REVERSE MATHEMATICS

Published online by Cambridge University Press:  09 September 2019

ANDRÉ NIES  and
PAUL SHAFER
ANDRÉ NIES
Affiliation:
SCHOOL OF COMPUTER SCIENCE UNIVERSITY OF AUCKLAND PRIVATE BAG92019AUCKLAND, NEW ZEALAND E-mail: [email protected]: https://www.cs.auckland.ac.nz/~nies/
PAUL SHAFER
Affiliation:
SCHOOL OF MATHEMATICS UNIVERSITY OF LEEDS LEEDS, LS2 9JT, UK E-mail: [email protected]: http://www1.maths.leeds.ac.uk/~matpsh/
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the strength of a randomness notion 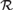${\cal R}$ as a set-existence principle in second-order arithmetic: for each Z there is an X that is 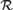${\cal R}$-random relative to Z. We show that the equivalence between 2-randomness and being infinitely often C-incompressible is provable in 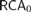$RC{A_0}$. We verify that 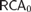$RC{A_0}$ proves the basic implications among randomness notions: 2-random 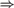$\Rightarrow$ weakly 2-random 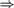$\Rightarrow$ Martin-Löf random 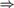$\Rightarrow$ computably random 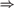$\Rightarrow$ Schnorr random. Also, over 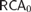$RC{A_0}$ the existence of computable randoms is equivalent to the existence of Schnorr randoms. We show that the existence of balanced randoms is equivalent to the existence of Martin-Löf randoms, and we describe a sense in which this result is nearly optimal.

Keywords

Primary 03B3003D3203F3568Q30computability theoryreverse mathematicsalgorithmic randomnessKolmogorov complexity
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 271 - 299
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ambos-Spies, K. and Kučera, A., Randomness in computability theory, Computability Theory and Its Applications: Current Trends and Open Problems (Boulder, CO, 1999) (Cholak, P. A., Lempp, S., Lerman, M., and Shore, R. A., editors), Contemporary Mathematics, vol. 257, American Mathematical Society, Providence, RI, 2000, pp. 1–14.Google Scholar
Avigad, J., Dean, E. T., and Rute, J., Algorithmic randomness, reverse mathematics, and the dominated convergence theorem. Annals of Pure and Applied Logic, vol. 163 (2012), no. 12, pp. 1854–1864.CrossRefGoogle Scholar
Barmpalias, G., Downey, R., and Ng, K. M., Jump inversions inside effectively closed sets and applications to randomness, this Journal, vol. 76 (2011), no. 2, pp. 491–518.Google Scholar
Bauwens, B., Prefix and plain Kolmogorov complexity characterizations of 2-randomness: Simple proofs. Archive for Mathematical Logic, vol. 54 (2015), no. 5–6, pp. 615–629.CrossRefGoogle Scholar
Bienvenu, L., Day, A. R., Greenberg, N., Kučera, A., Miller, J. S., Nies, A., and Turetsky, D., Computing K-trivial sets by incomplete random sets. Bulletin of Symbolic Logic, vol. 20 (2014), no. 1, pp. 80–90.CrossRefGoogle Scholar
Bienvenu, L., Muchnik, A., Shen, A., and Vereshchagin, N., Limit complexities revisited. Theory of Computing Systems, vol. 47 (2010), no. 3, pp. 720–736.CrossRefGoogle Scholar
Bienvenu, L., Patey, L., and Shafer, P., On the logical strengths of partial solutions to mathematical problems. Transactions of the London Mathematical Society, vol. 4 (2017), no. 1, pp. 30–71.CrossRefGoogle Scholar
Brattka, V., Gherardi, G., and Hölzl, R., Las Vegas computability and algorithmic randomness, 32nd International Symposium on Theoretical Aspects of Computer Science (Mayr, E. W. and Ollinger, N., editors), Leibniz International Proceedings in Informatics, vol. 30, Schloss Dagstuhl. Leibniz-Zentrum für Informatik, Wadern, 2015, pp. 130–142.Google Scholar
Brattka, V., Hendtlass, M., and Kreuzer, A. P., On the uniform computational content of computability theory. Theory of Computing Systems, vol. 61 (2017), no. 4, pp. 1376–1426.CrossRefGoogle Scholar
Brattka, V. and Pauly, A., On the algebraic structure of Weihrauch degrees. Logical Methods in Computer Science, vol. 14 (2018), no. 4, pp. 1–36.Google Scholar
Cholak, P., Greenberg, N., and Miller, J. S., Uniform almost everywhere domination, this Journal, vol. 71 (2006), no. 3, pp. 1057–1072.Google Scholar
Conidis, C. J., Effectively approximating measurable sets by open sets. Theoretical Computer Science, vol. 428 (2012), pp. 36–46.CrossRefGoogle Scholar
Conidis, C. J. and Slaman, T. A., Random reals, the rainbow Ramsey theorem, and arithmetic conservation, this Journal, vol. 78 (2013), no. 1, pp. 195–206.Google Scholar
Csima, B. F. and Mileti, J. R., The strength of the rainbow Ramsey theorem, this Journal, vol. 74 (2009), no. 4, pp. 1310–1324.Google Scholar
Day, A. R. and Miller, J. S., Density, forcing, and the covering problem. Mathematical Research Letters, vol. 22 (2015), no. 3, pp. 719–727.CrossRefGoogle Scholar
Demuth, O., Constructive pseudonumbers. Commentationes Mathematicae Universitatis Carolinae, vol. 16 (1975), pp. 315–331, (Russiand).Google Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.CrossRefGoogle Scholar
Figueira, S., Hirschfeldt, D. R., Miller, J. S., Ng, K. M., and Nies, A., Counting the changes of random ${\rm{\Delta }}_2^0$sets. Journal of Logic and Computation, vol. 25 (2015), no. 4, pp. 1073–1089.CrossRefGoogle Scholar
Franklin, J. N. Y. and Ng, K. M., Difference randomness. Proceedings of the American Mathematical Society, vol. 139 (2011), no. 1, pp. 345–360.CrossRefGoogle Scholar
Friedman, H., Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), vol. 1, Canadian Mathematical Congress, Vancouver, 1975, pp. 235–242.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998, Second printing.Google Scholar
Hinman, P. G., A survey of Mučnik and Medvedev degrees. Bulletin of Symbolic Logic, vol. 18 (2012), no. 2, pp. 161–229.CrossRefGoogle Scholar
Jockusch, C. G. Jr. and Soare, R. I., .${\rm{\Pi }}_1^0$ classes and degrees of theories. Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
Kučera, A., Measure, ${\rm{\Pi }}_1^0$-classes and complete extensions of PA, Recursion Theory Week (Oberwolfach, 1984) (Ebbinghaus, H.-D., Müller, G. H., and Sacks, G. E., editors), Lecture Notes in Mathematics, vol. 1141, Springer, Berlin, 1985, pp. 245–259.CrossRefGoogle Scholar
Kučera, A., An alternative, priority-free, solution to Post’s problem, Mathematical Foundations of Computer Science, 1986 (Bratislava, 1986) (Gruska, J., Rovan, B., and Wiedermann, J., editors), Lecture Notes in Computer Science, vol. 233, Springer, Berlin, 1986, pp. 493–500.CrossRefGoogle Scholar
Kučera, A. and Nies, A., Demuth randomness and computational complexity. Annals of Pure and Applied Logic, vol. 162 (2011), no. 7, pp. 504–513.CrossRefGoogle Scholar
Kurtz, S. A., Randomness and genericity in the degrees of unsolvability, Ph.D. thesis, University of Illinois at Urbana-Champaign, 1981, p. 138.Google Scholar
Martin-Löf, P., On the notion of randomness, Intuitionism and Proof Theory (Proc. Conf., Buffalo, N.Y., 1968) (Kino, A., Myhill, J., and Vesley, R. E., editors), North-Holland, Amsterdam, 1970, pp. 73–78.Google Scholar
Miller, J. S., personal communication.Google Scholar
Miller, J. S., Every 2-random real is Kolmogorov random, this Journal, vol. 69 (2004), no. 3, pp. 907–913.Google Scholar
Miller, J. S. and Nies, A., Randomness and computability: Open questions. Bulletin of Symbolic Logic, vol. 12 (2006), no. 3, pp. 390–410.CrossRefGoogle Scholar
Miyabe, K., Muchnik degrees and Medvedev degrees of randomness notions, Proceedings of the 14th and 15th Asian Logic Conferences (Kim, B., Brendle, J., Lee, G., Liu, F., Ramanujam, R., Srivastava, S. M., Tsuboi, A., and Yu, L., editors), World Scientific Publishing, Hackensack, NJ, 2019, pp. 108–128.Google Scholar
Miyabe, K., Nies, A., and Zhang, J., Using almost-everywhere theorems from analysis to study randomness. Bulletin of Symbolic Logic, vol. 22 (2016), no. 3, pp. 305–331.CrossRefGoogle Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Nies, A., Stephan, F., and Terwijn, S. A., Randomness, relativization and Turing degrees, this Journal, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar
Nies, A., Triplett, M. A., and Yokoyama, K., The reverse mathematics of theorems of Jordan and Lebesgue, preprint, 2017, arXiv:1704.00931.Google Scholar
Schnorr, C.-P., A unified approach to the definition of random sequences. Mathematical Systems Theory, vol. 5 (1971), pp. 246–258.CrossRefGoogle Scholar
Schnorr, C.-P., Zufälligkeit und Wahrscheinlichkeit. Eine algorithmische Begründung der Wahrscheinlichkeitstheorie, Lecture Notes in Mathematics, vol. 218, Springer-Verlag, Berlin-New York, 1971.CrossRefGoogle Scholar
Simpson, S. G., Mass problems and randomness. Bulletin of Symbolic Logic, vol. 11 (2005), no. 1, pp. 1–27.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge; Association for Symbolic Logic, Poughkeepsie, NY, 2009.CrossRefGoogle Scholar
Simpson, S. G., Mass problems associated with effectively closed sets. Tohoku Mathematical Journal. Second Series, vol. 63 (2011), no. 4, pp. 489–517.CrossRefGoogle Scholar
Slaman, T. A., .${{\rm{\Sigma }}_n}$-bounding and ${{\rm{\Delta }}_n}$-induction. Proceedings of the American Mathematical Society, vol. 132 (2004), no. 8, pp. 2449–2456.CrossRefGoogle Scholar
Slaman, T. A., The first-order fragments of second-order theories, CiE 2011, 2011.Google Scholar
Yu, X., Lebesgue convergence theorems and reverse mathematics. Mathematical Logic Quarterly, vol. 40 (1994), no. 1, pp. 1–13.CrossRefGoogle Scholar
Yu, X. and Simpson, S. G., Measure theory and weak König’s lemma. Archive for Mathematical Logic, vol. 30 (1990), no. 3, pp. 171–180.CrossRefGoogle Scholar